Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - нет. Эта геометрическая фигура привлекает внимание многих учащихся, так как имеет свои особенности, среди которых равенство накрест лежащих углов.
Равенство накрест лежащих углов в трапеции - это особенность, которая обусловлена тем, что стороны трапеции являются параллельными. Если от одной параллельной стороны откладывается перпендикуляр, соединяющий ее с противоположной стороной, то получаются два накрест лежащих угла. Эти углы являются равными, что можно проверить различными способами.
Один из способов проверки равенства накрест лежащих углов - использование свойства параллельных прямых, которое заключается в следующем: если прямая пересекает две параллельные прямые, то nакрест лежащие углы будут равными.
Другой способ проверки заключается в понимании свойств трапеции. В трапеции снова используется особенность параллельных прямых. Перпендикуляр из вершины трапеции к основанию разделяет ее на два прямоугольных треугольника. В этих треугольниках каждый из углов, образованных основанием и боковой стороной, равен комплиментарному накрест лежащему углу, что доказывает их равенство.
Определение трапеции и ее элементы
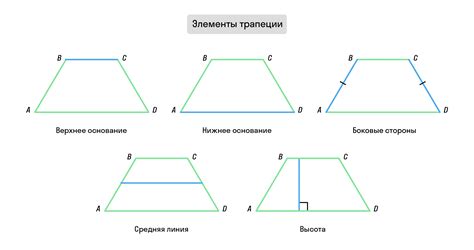
- Боковые стороны - это две не параллельные стороны трапеции.
- Основания - это параллельные стороны трапеции. Обозначаются как а и b.
- Вершины - это четыре точки пересечения сторон трапеции.
- Углы - это две пары углов, лежащих по одну сторону при не параллельных сторонах. Обозначаются как A, B, C и D.
- Диагонали - это отрезки, соединяющие противоположные вершины трапеции.
Важно отметить, что в рамках данной статьи мы сосредоточимся на особенности равенства накрест лежащих углов в трапеции и способы их проверки.
Ключевая особенность трапеции: накрест лежащие углы

Существуют различные способы доказательства этой особенности. Один из них основан на использовании параллельных прямых, проведенных через вершины трапеции. Другой способ основан на применении свойств углов, диагоналей и параллельных линий в трапеции.
Зная ключевую особенность трапеции - равенство накрест лежащих углов, мы можем использовать ее для решения задач, связанных с нахождением углов и сторон трапеции. Например, для вычисления угла в трапеции можно использовать равные накрест лежащие углы и свойства треугольников.
Зависимость накрест лежащих углов от типа трапеции

Существует несколько типов трапеций, у каждого из которых имеются свои особенности. Зависимость накрест лежащих углов от типа трапеции может быть выражена следующим образом:
- Прямоугольная трапеция:
- Равнобокая трапеция:
- Равнобедренная трапеция:
- Произвольная трапеция:
В прямоугольной трапеции накрест лежащие углы (угол между боковой стороной и основанием) всегда равны друг другу и являются прямыми углами.
Равнобокая трапеция - это трапеция, у которой боковые стороны равны друг другу. Накрест лежащие углы в равнобокой трапеции равны друг другу.
Равнобедренная трапеция, как следует из названия, имеет два равных угла. Накрест лежащие углы в равнобедренной трапеции также равны друг другу.
В произвольной трапеции накрест лежащие углы могут быть разными и зависят от величины остальных углов и длин сторон.
Связь накрест лежащих углов с дополнительными углами
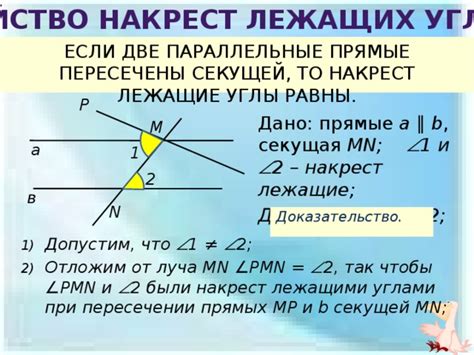
Дополнительным углом к данному углу является угол, сумма которого с данным углом равна 180 градусов. В трапеции существует несколько дополнительных углов:
- Дополнительный угол к верхнему основанию равен нижнему основанию;
- Дополнительный угол к нижнему основанию равен верхнему основанию;
- Дополнительные углы к боковым сторонам равны между собой.
Из свойств накрест лежащих углов следует, что:
- Сумма накрест лежащих углов трапеции всегда равна 180 градусов;
- Угол, смежный с углом, дополнительным к верхнему основанию, равен углу, дополнительному к нижнему основанию;
- Угол, смежный с углом, дополнительным к боковой стороне, равен боковому углу.
Таким образом, углы трапеции взаимосвязаны через накрест лежащие и дополнительные углы. Это свойство используется для решения задач на нахождение неизвестных углов и сторон в трапеции.
Проверка равенства накрест лежащих углов в трапеции

В трапеции можно выделить две пары накрест лежащих углов: верхние и нижние. Углы, лежащие на одной стороне трапеции и находящиеся по разные стороны от этой стороны, называются накрест лежащими.
Чтобы проверить равенство накрест лежащих углов в трапеции, нужно знать следующие правила:
- Верхние накрест лежащие углы трапеции равны между собой, то есть ∠A = ∠C и ∠B = ∠D.
- Нижние накрест лежащие углы трапеции также равны между собой, то есть ∠E = ∠G и ∠F = ∠H.
- Верхние и нижние накрест лежащие углы трапеции дополняют друг друга до 180 градусов, то есть ∠A + ∠C = 180° и ∠B + ∠D = 180°.
Для проверки равенства накрест лежащих углов в трапеции можно использовать известные значения углов или применить соответствующие геометрические методы.
Знание свойств и правил равенства накрест лежащих углов в трапеции позволяет более точно анализировать и решать геометрические задачи, связанные с этой фигурой.
Примеры задач с проверкой равенства накрест лежащих углов
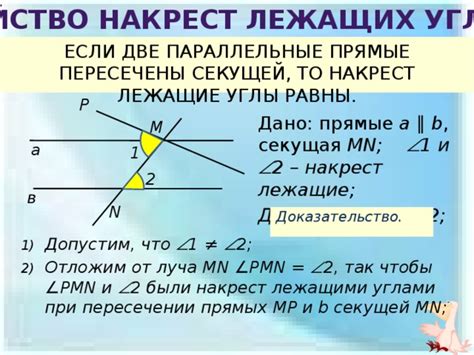
Для проверки равенства накрест лежащих углов в трапеции можно использовать следующие методы:
- Метод 1: Используйте свойства и теоремы о трапеции
- Метод 2: Используйте свойства параллельных прямых
- Метод 3: Используйте измерение углов



