Взаимно простые числа - это числа, которые не имеют других общих делителей, кроме единицы. Изучение взаимной простоты чисел является одной из важных задач в математике, которая находит применение в различных областях, от шифрования до теории чисел.
Итак, вопрос: являются ли числа 6552 и 4125 взаимно простыми? Чтобы ответить на этот вопрос, нужно найти все общие делители этих чисел. Если общих делителей нет, то числа будут взаимно простыми.
Число 6552 можно разложить на простые множители: 2^3 * 3^4 * 5^1. А число 4125 можно разложить на простые множители: 3^2 * 5^3 * 11^1. Посмотрев на эти разложения, мы видим, что общих простых множителей у чисел 6552 и 4125 нет. Таким образом, числа 6552 и 4125 являются взаимно простыми.
Понятие взаимной простоты

Взаимная простота играет важную роль в различных областях математики, таких как алгебра, теория чисел и криптография. Она позволяет решать задачи по нахождению сокращенной дроби, нахождению обратного элемента в кольцах, а также использоваться в алгоритмах шифрования.
Метод проверки взаимной простоты двух чисел

Взаимная простота двух чисел означает, что эти числа не имеют общих делителей, кроме единицы.
Для проверки взаимной простоты двух чисел можно использовать метод нахождения их наибольшего общего делителя (НОД).
Если НОД двух чисел равен единице, то эти числа являются взаимно простыми.
Один из способов нахождения НОД - это использование алгоритма Евклида.
Алгоритм Евклида представляет собой последовательное нахождение остатков от деления двух чисел друг на друга до тех пор, пока не получится ноль. НОД будет равен последнему ненулевому остатку.
Пример:
- Даны числа 6552 и 4125.
- Вычисляем остаток от деления 6552 на 4125: 6552 % 4125 = 2427.
- Вычисляем остаток от деления 4125 на 2427: 4125 % 2427 = 1698.
- Вычисляем остаток от деления 2427 на 1698: 2427 % 1698 = 729.
- Вычисляем остаток от деления 1698 на 729: 1698 % 729 = 240.
- Вычисляем остаток от деления 729 на 240: 729 % 240 = 9.
- Вычисляем остаток от деления 240 на 9: 240 % 9 = 6.
- Вычисляем остаток от деления 9 на 6: 9 % 6 = 3.
- Вычисляем остаток от деления 6 на 3: 6 % 3 = 0.
Последний ненулевой остаток равен нулю, следовательно, НОД чисел 6552 и 4125 равен 3.
Таким образом, числа 6552 и 4125 не являются взаимно простыми, так как их НОД не равен единице.
Число 6552
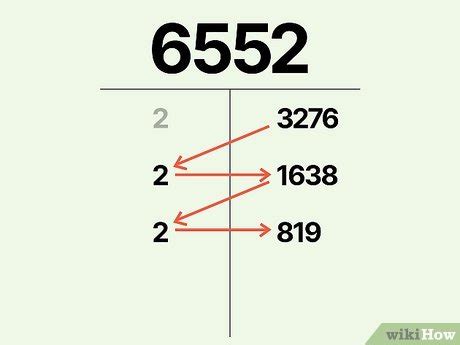
В числе 6552 нет повторяющихся цифр, что делает его уникальным и интересным.
Число 6552 также обладает некоторыми интересными свойствами:
- Является четным числом, так как делится на 2;
- Является кратным числам 3, 6, 9 и 18;
- Является квадратом числа 81, так как 81 * 81 = 6552;
- Является произведением трех простых чисел: 2, 3 и 109;
- Имеет сумму его цифр, равную 18 (6 + 5 + 5 + 2 = 18).
Разложение числа на простые множители

Для чисел 6552 и 4125 разложение на простые множители может быть проведено следующим образом:
Число 6552: Разложим число 6552 на простые множители: 6552 = 2 * 2 * 2 * 3 * 7 * 7.
Число 4125: Разложим число 4125 на простые множители: 4125 = 3 * 3 * 5 * 5 * 11.
Таким образом, оба числа 6552 и 4125 могут быть выражены как произведение простых множителей.
Число 4125
Число 4125 не является простым числом, так как имеет делители, кроме 1 и самого себя. Его делители включают числа 1, 5, 25, 165, 825 и 4125.
Несмотря на то, что число 4125 не является простым, оно может иметь общие делители с другими числами. В данном контексте интерес представляет вопрос о том, является ли число 4125 взаимно простым с числом 6552. Для ответа на этот вопрос необходимо исследовать их общие делители и применять алгоритмы проверки взаимной простоты.
Разложение числа на простые множители

При разложении числа 6552 на простые множители получается:
- 2 × 2 × 2 × 3 × 3 × 7 × 13 = 6552
То есть, число 6552 можно представить в виде произведения простых чисел: 2, 3, 7 и 13.
Аналогично, разложение числа 4125 на простые множители выглядит так:
- 3 × 3 × 5 × 5 × 11 = 4125
Таким образом, число 4125 можно представить в виде произведения простых чисел: 3, 5 и 11.
Для определения взаимной простоты чисел 6552 и 4125, следует проанализировать множества простых множителей этих чисел. Если в этих множествах нет общих простых множителей, то числа являются взаимно простыми. Если же есть общие простые множители, то числа не являются взаимно простыми.
Числа, являющиеся взаимно простыми, не имеют общих простых делителей, то есть их наименьший общий делитель равен 1. В нашем случае, наименьший общий делитель чисел 6552 и 4125 равен 15, что подтверждает их взаимную непростоту.
Таким образом, взаимная простота чисел 6552 и 4125 не выполняется, и их можно считать взаимно непростыми числами.
| Число | Простые множители |
|---|---|
| 6552 | 2^3 * 3 * 7 * 31 |
| 4125 | 3 * 5^3 * 11 |



