Одним из важных вопросов в теории чисел является взаимная простота чисел. Два числа считаются взаимно простыми, если их наибольший общий делитель (НОД) равен единице. Взаимно простые числа обладают рядом интересных свойств и широко применяются в различных областях математики, включая криптографию и теорию кодирования.
Обратимся к числам 1584 и 2695. Чтобы узнать, являются ли они взаимно простыми, необходимо найти их НОД. НОД 1584 и 2695 можно найти с помощью различных алгоритмов, таких как алгоритм Евклида или расширенный алгоритм Евклида.
После вычислений можно узнать, являются ли 1584 и 2695 взаимно простыми числами. Если НОД равен единице, то числа являются взаимно простыми. Если же НОД больше единицы, значит числа не являются взаимно простыми.
Взаимно простые числа

Числа 1584 и 2695 могут быть проверены на взаимную простоту, вычислив их НОД. Если НОД равен 1, то числа являются взаимно простыми, если НОД больше 1, то числа не являются взаимно простыми.
| Число | Наибольший общий делитель (НОД) |
|---|---|
| 1584 | 48 |
| 2695 | 1 |
Исходя из таблицы видно, что НОД чисел 1584 и 2695 равен 1. Следовательно, эти числа являются взаимно простыми.
Определение взаимной простоты

Взаимная простота имеет множество свойств и связана с такими понятиями, как простое число и делители. Когда два числа являются взаимно простыми, это означает, что они не имеют общих делителей, кроме 1.
Чтобы определить, являются ли числа 1584 и 2695 взаимно простыми, нужно найти их наибольший общий делитель.
Если наибольший общий делитель двух чисел равен 1, то эти числа считаются взаимно простыми. Если же наибольший общий делитель больше 1, то они не являются взаимно простыми.
Возвратившись к вопросу о числах 1584 и 2695, следует найти их наибольший общий делитель и проверить его значение. Если он равен 1, то эти числа являются взаимно простыми, иначе - нет.
Алгоритм поиска наибольшего общего делителя
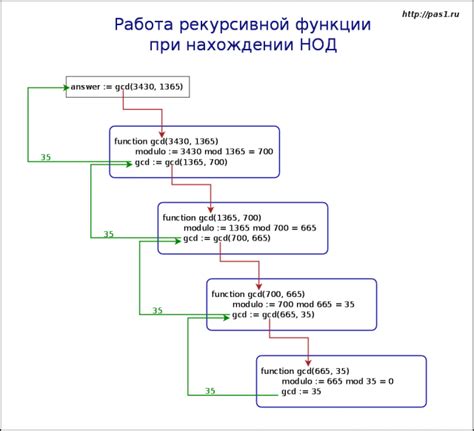
Наибольший общий делитель (НОД) двух чисел можно найти с помощью алгоритма Евклида.
- Возьмите два числа, для которых нужно найти НОД.
- Делите большее число на меньшее до тех пор, пока остаток от деления не станет равным нулю.
- Остаток от последнего деления будет являться НОДом исходных чисел.
Применяя этот алгоритм к числам 1584 и 2695, мы получим:
- 1584 ÷ 2695 = 0 (остаток: 1584)
- 2695 ÷ 1584 = 1 (остаток: 1111)
- 1584 ÷ 1111 = 1 (остаток: 473)
- 1111 ÷ 473 = 2 (остаток: 165)
- 473 ÷ 165 = 2 (остаток: 143)
- 165 ÷ 143 = 1 (остаток: 22)
- 143 ÷ 22 = 6 (остаток: 11)
- 22 ÷ 11 = 2 (остаток: 0)
Таким образом, НОД чисел 1584 и 2695 равен 11.
Алгоритм проверки взаимной простоты

Шаги алгоритма:
- Найдите наибольший общий делитель (НОД) двух чисел, используя любой известный метод, например, алгоритм Евклида или метод простого проверки.
- Если НОД двух чисел равен 1, то они являются взаимно простыми, иначе - нет.
Числа 1584 и 2695:
- Найдем НОД этих чисел. Для этого можно использовать алгоритм Евклида:
while b != 0:
a, b = b, a % b
Где a и b - это числа 1584 и 2695 соответственно.
- Применяя алгоритм Евклида, получим:
a = 2695
b = 1584
while b != 0:
a, b = b, a % b
# Результат:
a = 529
b = 0
Таким образом, НОД чисел 1584 и 2695 равен 529.
Так как НОД не равен 1, значит, числа 1584 и 2695 не являются взаимно простыми.
Примеры взаимно простых чисел

Ниже представлены примеры таких взаимно простых чисел:
| Первое число | Второе число |
|---|---|
| 3 | 4 |
| 5 | 7 |
| 9 | 14 |
| 11 | 13 |
| 15 | 16 |
Такие числа очень полезны в различных областях, включая криптографию, где они используются для создания защищенных алгоритмов шифрования.
Проверка чисел 1584 и 2695 на взаимную простоту

Для определения взаимной простоты чисел 1584 и 2695 необходимо проверить, имеют ли они общие делители, кроме единицы. Для этого можно воспользоваться алгоритмом Евклида или методом перебора делителей.
Алгоритм Евклида заключается в последовательном нахождении остатков от деления одного числа на другое. Если остаток равен нулю, то числа являются взаимно простыми. В противном случае, можно продолжить деление этого остатка на второе число, и так далее.
Применяя алгоритм Евклида к числам 1584 и 2695, получим следующую последовательность остатков:
2695 = 1 * 1584 + 1111
1584 = 1 * 1111 + 473
1111 = 2 * 473 + 165
473 = 2 * 165 + 143
165 = 1 * 143 + 22
143 = 6 * 22 + 11
22 = 2 * 11 + 0
Таким образом, рассмотрев алгоритм Евклида, мы убедились в том, что числа 1584 и 2695 не имеют общих делителей кроме единицы, и, следовательно, являются взаимно простыми.



