Равносторонний треугольник – одна из самых простых геометрических фигур, а его особенность заключается в том, что все его стороны и углы равны. Это свойство привлекает внимание многих людей и вызывает интерес к данным треугольникам. Однако, одно из наиболее распространенных заблуждений о равносторонних треугольниках заключается в утверждении, что все равносторонние треугольники подобны. Давайте разберемся, действительно ли эта информация является правдой или всего лишь мифом.
Для начала стоит вспомнить определение подобных фигур. Две фигуры считаются подобными, если они имеют одинаковую форму, но могут отличаться по размеру. Основное условие подобия - углы с одинаковыми мерами должны быть расположены в обоих фигурах соответственно и параллельно. Но если все равносторонние треугольники являются фигурами с одинаковыми сторонами и углами, то почему их нельзя считать подобными?
Секрет кроется в том, что для равносторонних треугольников условие подобия не выполняется. Все равносторонние треугольники действительно имеют одинаковую форму, но углы в них не параллельны и не соответствуют условию подобия. Подобие треугольников имеет глубокое математическое объяснение и непосредственно связано с их углами, длинами сторон и отношением этих параметров.
Определение равностороннего треугольника

Из определения равностороннего треугольника следует, что все его углы равны 60 градусов. Это свойство обуславливает особые характеристики и особый вид треугольника. Благодаря равным сторонам, равносторонний треугольник имеет три симметричных оси симметрии относительно каждой стороны и центра. Эти оси симметрии проходят через точки деления сторон пополам и точку-центр.
Равносторонний треугольник также обладает уникальными свойствами при построении: любая из высот является медианой и биссектрисой одновременно. Более того, ортоцентр, центр окружности, описанной вокруг треугольника и центр вписанной окружности совпадают в равностороннем треугольнике.
Признаки подобия треугольников
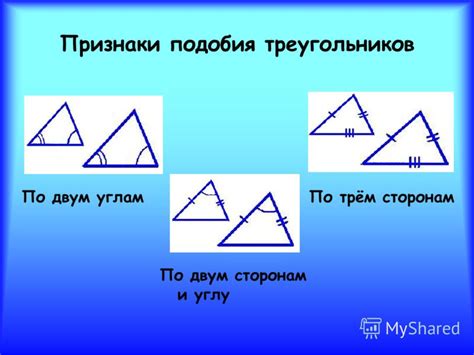
Для определения подобия треугольников можно использовать следующие признаки:
- Угловой признак: Если два треугольника имеют соответственные углы, равные друг другу, то они подобны.
- Признаки по длинам сторон:
- Признак совпадения сторон: Если два треугольника имеют все стороны, равные соответственно, то они подобны.
- Пропорциональность сторон: Если отношение длин сторон одного треугольника к длинам соответственных сторон другого треугольника постоянно, то треугольники подобны.
- Признак совместимости пропорций: Если отношение длины одной стороны одного треугольника к длине соответствующей стороны другого треугольника равно отношению длины другой стороны первого треугольника к длине соответствующей стороны второго треугольника, то треугольники подобны.
Таким образом, все равносторонние треугольники являются одним из случаев подобия треугольников, но подобие возможно и среди других треугольников, если выполняются указанные признаки.
Доказательство подобия равносторонних треугольников

Если мы возьмем два равносторонних треугольника, то можно доказать, что они будут подобны друг другу. Для доказательства будем использовать геометрическую конструкцию.
| 1. Шаг | Выберем любую сторону одного треугольника и проведем прямую, которая будет перпендикулярна к этой стороне и проходить через противоположный угол треугольника. |
| 2. Шаг | Соединим конец проведенной прямой с вершиной треугольника, являющейся смежной с выбранной стороной. |
| 3. Шаг | Таким образом, получим треугольник, у которого одна сторона равна одной стороне изначального треугольника, а две другие стороны совпадают с отрезками, проведенными из вершины треугольника. |
| 4. Шаг | При этом, углы, заключенные между сторонами нового треугольника, будут являться прямыми, так как прямая была проведена перпендикулярно одной из сторон изначального треугольника. |
Исходя из этих шагов, можно заключить, что у получившегося треугольника все углы будут прямыми, а две его стороны будут равны соответствующим сторонам исходного треугольника.
Таким образом, мы доказали, что два равносторонних треугольника являются подобными, то есть имеют одинаковую форму, но могут отличаться размерами. Это является фундаментальным свойством равносторонних треугольников.
Свойства равносторонних треугольников

1. Подобие треугольников
Самое очевидное свойство равностороннего треугольника заключается в том, что все равносторонние треугольники подобны друг другу. Подобие треугольников означает, что у них соответствующие углы равны, а соотношение между длинами сторон одинаково.
2. Равнобедренность
Каждая сторона равностороннего треугольника одновременно является его высотой и медианой. Это означает, что треугольник является равнобедренным, то есть у него две равные стороны и два равных угла.
3. Сумма углов
Сумма всех углов в равностороннем треугольнике равна 180 градусам. Учитывая, что каждый угол равен 60 градусам, мы можем утверждать, что каждый угол треугольника равносторонний.
4. Площадь треугольника
Площадь равностороннего треугольника можно вычислить по формуле S = (a^2 * sqrt(3)) / 4, где a - длина стороны треугольника. Эта формула позволяет нам легко найти площадь, зная только длину стороны треугольника.
5. Центр вписанной окружности
Центр вписанной окружности равностороннего треугольника совпадает с центром треугольника и пересекает его перпендикулярно. Радиус этой окружности равен одной трети длины стороны треугольника.
- Свойство 1: подобие треугольников;
- Свойство 2: равнобедренность;
- Свойство 3: сумма углов;
- Свойство 4: площадь треугольника;
- Свойство 5: центр вписанной окружности.
Примеры применения равносторонних треугольников

1. Строительство: Равносторонние треугольники используются в строительстве для обеспечения прочности и стабильности конструкций. Они часто применяются в угловых опорах, а также в основаниях зданий и мостов.
2. Навигация: Равносторонние треугольники используются в навигации для определения расстояний и направлений. Они помогают морякам и пилотам определить свое местоположение и найти кратчайший путь к цели.
3. Геодезия и картография: Равносторонние треугольники являются важным инструментом в геодезии и картографии. Они используются для измерения расстояний, построения карт и определения формы Земли.
4. Игры и развлечения: Равносторонние треугольники встречаются и в различных играх и головоломках. Например, в головоломке "танграм" используются треугольные элементы, среди которых присутствуют и равносторонние треугольники.
5. Дизайн и искусство: Равносторонние треугольники могут быть использованы в дизайне и искусстве для создания симметричных и гармоничных композиций. Они могут служить основой для построения геометрических фигур и украшений.
Применение равносторонних треугольников не ограничивается данным списком. Они находят свое применение во многих других областях, подтверждая свою универсальность и важность в геометрии и практической деятельности человека.
1. Все равносторонние треугольники имеют одинаковую форму. Равносторонний треугольник состоит из трех равных сторон и трех равных углов. Это означает, что все его углы равны 60 градусам, а его стороны имеют одинаковую длину. Благодаря этим свойствам, равносторонний треугольник всегда будет иметь одинаковую форму, независимо от его размера.
3. Подобные фигуры имеют одинаковые соотношения между углами. Также следует отметить, что подобные фигуры имеют одинаковые соотношения между углами. Это означает, что если два равносторонних треугольника имеют одинаковые углы, то они будут подобны. Все равносторонние треугольники имеют углы, которые равны 60 градусам. Другими словами, углы равносторонних треугольников будут иметь одинаковые соотношения.



