Математика – это наука о числах, и в процессе изучения чисел возникает вопрос о том, как учесть их знак при сравнении и оперировании. Одним из ответов на этот вопрос является знаковая функция или модуль числа. Модуль извлекает абсолютное значение числа, игнорируя его знак. Однако, не всегда модуль числа равен самому числу, и в этой статье мы рассмотрим различные случаи и свойства знаковой функции.
Если число положительное, то его модуль будет равен самому числу. Например, модуль числа 5 равен 5. Это свидетельствует о том, что при оперировании с положительными числами можно пренебрегать знаком числа и сосредоточиться только на его абсолютном значении.
Однако, если число отрицательное, то его модуль будет равен отрицательному числу с обратным знаком. Например, модуль числа -5 равен 5. Это означает, что для отрицательных чисел знаковая функция превращает их в положительные числа. Такой подход позволяет учитывать и оперировать с отрицательными числами наравне с положительными.
Роль знаковой функции в математике
Знаковая функция |x| определяется следующим образом:
Если x > 0, то |x| = x.
Если x < 0, то |x| = -x.
Если x = 0, то |x| = 0.
Использование знаковой функции позволяет исправить основную проблему с числами - их знак. В математических операциях с числами, особенно в алгебре и арифметике, знаковая функция позволяет нам упростить выражения и избежать ошибок, связанных с изменением знака числа.
Кроме того, знаковая функция играет важную роль при решении уравнений и неравенств. Например, при решении уравнений с модулем необходимо рассмотреть два случая, когда модуль равен положительному значению и когда модуль равен отрицательному значению. Это позволяет нам найти все возможные значения переменной и найти корни уравнения.
В общем, знаковая функция является важным математическим инструментом, который помогает нам понять и работать с знаками чисел. Она находит свое применение не только в математике, но и в других науках, где используются числа и их знаки.
Определение модуля числа

Математически обозначается символом |x|, где x – число, для которого находим модуль. Если число положительное или нулевое, модуль совпадает с самим числом: |x| = x. Если число отрицательное, модуль равен противоположному по знаку числу: |x| = -x.
Например, для числа -5 модуль будет равен 5, так как это отрицательное число, и его противоположное по знаку значение – 5. А для числа 3 модуль будет равен 3, так как оно положительное и его модуль равен самому числу.
Модуль числа широко применяется в различных областях математики, физики и других наук. Он позволяет отбросить информацию о знаке числа и сосредоточиться только на его абсолютной величине. Также модуль числа используется для определения расстояния между числами и в решении уравнений и неравенств.
Особенности модуля положительных чисел
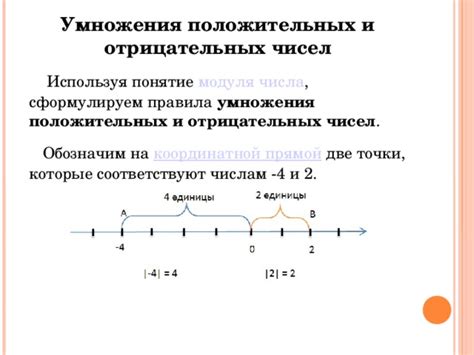
Одной из особенностей модуля положительных чисел является то, что для положительных чисел значение модуля совпадает со значением самого числа. Например, модуль числа 5 равен 5.
Модуль положительных чисел не изменяет их знак, так как уже положительные числа имеют положительный знак. Это отличается от случая с отрицательными числами, где модуль меняет знак на положительный. Например, модуль числа -5 также равен 5.
Модуль положительных чисел широко используется в различных областях математики, физики, информатики и других наук. Например, в геометрии модуль может использоваться для расчета расстояния между двумя точками, а в физике – для определения величины векторов.
| Число | Модуль числа |
|---|---|
| 5 | 5 |
Таким образом, модуль положительных чисел имеет одно и то же значение, что и само число, и не меняет его знак.
Особенности модуля отрицательных чисел
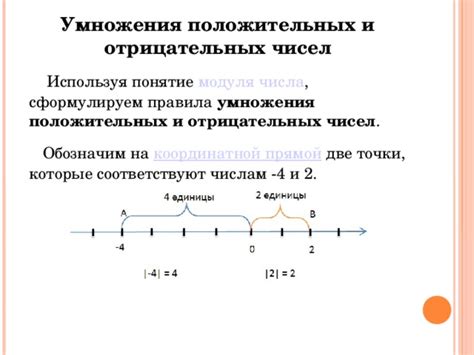
Модуль числа отражает его расстояние от нуля на числовой прямой. В большинстве случаев модуль числа равен самому числу, но в случае отрицательных чисел есть некоторые особенности.
Если число является отрицательным, то его модуль будет равен его абсолютной величине без знака. Например, модуль числа -5 будет равен 5.
Чтобы получить модуль отрицательного числа, можно использовать математическую функцию abs(). Эта функция возвращает абсолютную величину числа без знака.
Например:
| Число | Модуль |
|---|---|
| -5 | 5 |
| -10 | 10 |
| -15 | 15 |
Таким образом, модуль отрицательных чисел всегда будет равен их абсолютной величине, но без знака минус.
Знаковая функция в математике позволяет определить знак числа, но не используется для нахождения модуля числа. Для этой цели используется функция abs().
Различные способы нахождения модуля числа
Модуль числа представляет собой абсолютное значение числа, то есть его расстояние до нуля, и обозначается символом |x|.
Существуют различные способы нахождения модуля числа:
| Способ | Описание |
|---|---|
| 1. Использование условного оператора | Если число x больше или равно нулю, то модуль равен самому числу, иначе модуль равен противоположному значению числа. |
| 2. Выражение в виде квадратного корня из произведения числа на его противоположное значение | Модуль числа можно выразить в виде квадратного корня из произведения числа на его противоположное значение. |
| 3. Использование встроенных функций в языках программирования | Многие языки программирования предоставляют встроенные функции для вычисления модуля числа. Эти функции могут работать непосредственно с числами различных типов данных. |
Выбор способа нахождения модуля числа зависит от контекста и требуемой точности вычислений.
Примеры использования знаковой функции в математике
| Число | Знаковая функция |
|---|---|
| 5 | 1 |
| -2 | -1 |
| 0 | 0 |
Примеры использования знаковой функции:
- Определение знака числа
- Вычисление абсолютной величины
- Решение неравенств
Знаковая функция позволяет определить знак числа. Например, для числа -5 знаковая функция будет равна -1, что означает, что число отрицательное.
Знаковая функция позволяет вычислить абсолютное значение числа. Для любого числа x, как положительного, так и отрицательного, можно выразить его абсолютное значение как сумму самого числа и произведения его на знаковую функцию:
|x| = x * sign(x)
Знаковая функция позволяет решать неравенства в математике. Например, для решения неравенства x > 0 можно умножить обе части неравенства на знаковую функцию, получив следующее равносильное неравенство: sign(x) * x > 0.
1. Модуль числа позволяет нам оценить расстояние между числом и нулем на числовой оси. Это полезно, когда нам не важен знак числа, а важно его расстояние до нуля. Например, модуль разности двух чисел показывает, насколько они отличаются друг от друга.
2. Модуль числа используется для решения различных математических уравнений и неравенств. Например, модуль может использоваться для нахождения корней квадратного уравнения или для определения интервала значений переменной в неравенстве.
3. Модуль числа также может использоваться для определения амплитуды волны в физике. Амплитуда - это максимальное значение функции, а модуль позволяет нам получить это значение, игнорируя знак.
4. Модуль числа также может быть использован для определения расстояния между двумя точками на плоскости. Например, модуль разности координат точек на координатной плоскости покажет расстояние между этими точками.
В целом, модуль числа играет важную роль в математике и имеет множество применений. Он позволяет нам оценить абсолютное значение числа и использовать его для решения различных задач и проблем в различных областях.



