Движение тела по окружности является одним из основных механических движений, которое широко применяется в различных областях науки и техники. Изучение движения точки на окружности позволяет более глубоко понять основные законы физики и связь между различными физическими величинами.
Одним из важных аспектов при движении точки на окружности является изменение импульса. Импульс – это физическая величина, которая характеризует количество движения тела. Во время равномерного движения точки по окружности ее импульс будет изменяться в зависимости от момента времени и других факторов.
Изучение изменения импульса точки на окружности имеет большое практическое значение. Это позволяет оптимизировать движение тела, расчеты силы и скорости, а также предсказывать результаты экспериментов в различных областях науки и техники. Кроме того, такое исследование дает возможность понять взаимосвязь между импульсом и другими физическими параметрами, что помогает разрабатывать новые технологии и улучшать существующие.
Определение и свойства точки на окружности
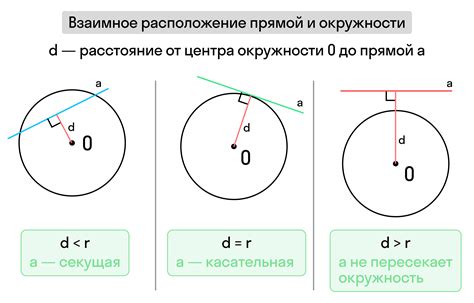
Свойства точек на окружности:
- Расстояние до центра: Расстояние от точки на окружности до центра окружности всегда равно радиусу окружности. Это свойство определяет основное отличие точек на окружности от точек внутри или вне окружности.
- Угол между радиусом и касательной: Если провести радиус окружности к точке на окружности и касательную к окружности в этой точке, то угол между ними будет прямым. Это свойство объясняет поведение луча света, падающего на плоскую зеркальную поверхность – он отражается так, что угол падения равен углу отражения.
- Симметричность: Точки на окружности всегда симметричны относительно оси симметрии, проходящей через центр окружности. Это означает, что если одна точка лежит на окружности, то ей соответствует вторая точка, симметричная первой относительно оси симметрии.
Точки на окружности широко используются в различных областях, включая геометрию, физику и компьютерную графику. Понимание их свойств помогает в решении задач, связанных с окружностями и их применением.
Понятие окружности и радиус
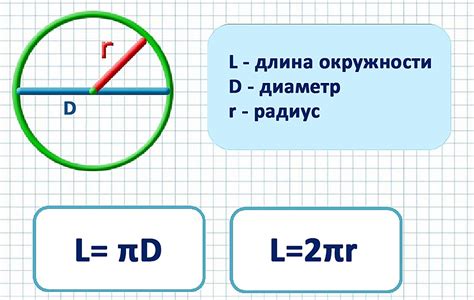
Радиус окружности - это расстояние от центра окружности до любой точки, лежащей на окружности. Обозначается буквой "r".
Радиус является важной характеристикой окружности, так как определяет ее размер. Длина окружности, также называемая окружностным периметром, равна произведению радиуса на удвоенное число "π" (пи).
Окружность и ее радиус находят применение в различных областях, таких как геометрия, физика, астрономия и т.д. Окружности часто встречаются в повседневной жизни - от колес автомобилей до короны солнечного затмения.
Определение точки на окружности
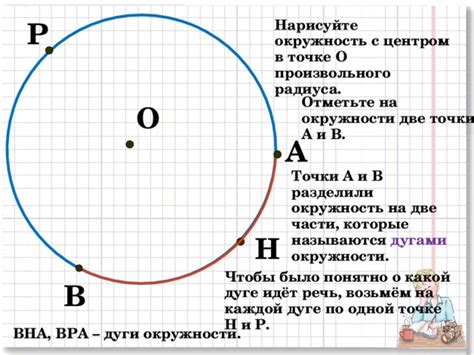
При изучении движения точки на окружности важно уметь определять текущее положение точки в зависимости от времени. Для определения точки на окружности используется геометрическое и тригонометрическое решение.
Геометрическое решение заключается в построении правильной окружности с заданным радиусом и центром, а затем определении положения точки на окружности в зависимости от времени. Например, если мы знаем, что точка начинает движение из начального положения, то при равномерном движении ее положение на окружности можно определить, зная угловую скорость и время движения.
Тригонометрическое решение основано на использовании тригонометрических функций, таких как синус и косинус. На основе этих функций определяются значения соответствующих угловых координат точки на окружности при заданном времени.
| Геометрическое решение | Тригонометрическое решение |
|---|---|
| Построение окружности | Использование тригонометрических функций |
| Определение положения точки | Вычисление угловых координат |
Равномерное движение и его характеристики
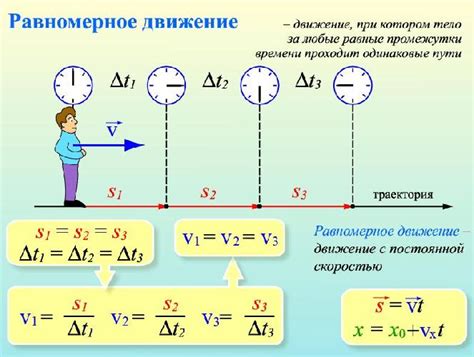
Характеристики равномерного движения:
| Характеристика | Определение |
|---|---|
| Скорость | Постоянная величина, равная отношению перемещения тела к промежутку времени, за которое это перемещение произошло. |
| Ускорение | Отсутствует, так как скорость всегда постоянна. |
| Путь | Длина пройденного телом пути за заданное время. |
| Время | Промежуток времени, за которое тело прошло заданный путь. |
Равномерное движение важно в физике, так как позволяет упростить анализ движений, сделать точные расчеты, а также применяется в различных технических и научных областях.
Определение равномерного движения
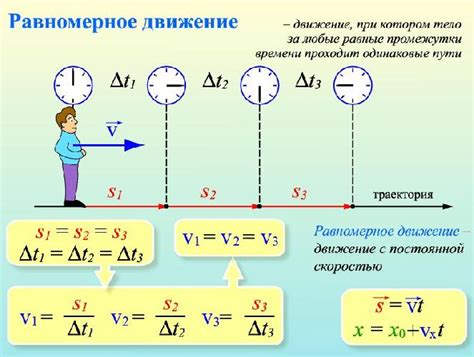
Равномерное движение представляет собой такое движение тела, при котором оно перемещается одинаковые расстояния за одинаковые промежутки времени. В этом случае скорость тела остается постоянной на всем пути.
Равномерное движение обладает следующими особенностями:
- Тело перемещается с постоянной скоростью.
- Расстояние, пройденное телом, пропорционально времени движения.
- График зависимости пройденного пути от времени является прямой линией.
- Ускорение тела равно нулю.
Такое движение часто встречается в повседневной жизни. Например, автомобиль, двигающийся по прямой дороге с постоянной скоростью, выполняет равномерное движение. Также великолепным примером является часовая стрелка, которая движется с постоянной скоростью.
Параметры равномерного движения
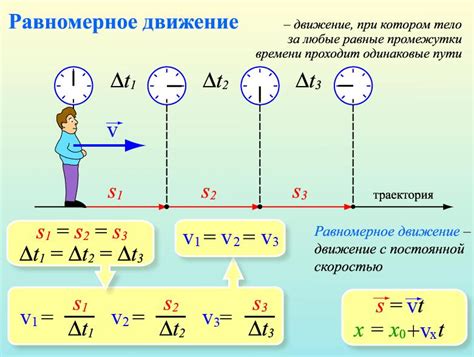
Основными параметрами равномерного движения являются:
| Параметр | Обозначение | Определение |
|---|---|---|
| Скорость | v | Отношение пройденного пути к затраченному времени: v = s / t |
| Пройденное расстояние | s | Расстояние между начальной и конечной точками движения |
| Время | t | Затраченное на движение время |
Скорость равномерного движения остается постоянной в течение всего перемещения. Она может выражаться в м/с, км/ч и других единицах измерения.
Пройденное расстояние зависит от скорости и времени. Чем больше скорость и время движения, тем дальше будет перемещаться точка на окружности.
Время - это параметр, который определяет длительность равномерного движения и измеряется в секундах.
Зная значения этих параметров, можно рассчитать один из них, зная остальные два. Например, время можно найти по формуле t = s / v, а пройденное расстояние - по формуле s = v * t.
Влияние точки на окружности на изменение импульса

Когда точка на окружности движется равномерно, ее скорость постоянна, но направление движения постоянно меняется. Это означает, что вектор скорости точки на окружности постоянно изменяется, а следовательно, и ее импульс.
При движении точки на окружности, изменение ее импульса зависит от направления радиуса, соединяющего центр окружности с точкой, и его длины. Если радиус изменяет свое направление, то изменение импульса точки будет происходить постоянно. Если радиус не изменяет свое направление, то изменение импульса точки будет нулевым.
Особо интересным случаем является движение точки по окружности радиусом r с постоянной скоростью. В этом случае радиус всегда перпендикулярен вектору скорости, и его длина не меняется. Такое движение называется равномерным движением по окружности. При таком движении изменение импульса точки будет нулевым, так как вектор скорости и радиус всегда перпендикулярны.
Таким образом, точка на окружности оказывает влияние на изменение импульса в зависимости от своего движения. При равномерном движении по окружности изменение импульса будет нулевым, а при других видах движения будет происходить постоянное изменение импульса.



