Шестиугольник – это геометрическая фигура с шестью сторонами и шестью углами. Шестиугольники могут быть выпуклыми или невыпуклыми, в зависимости от того, как расположены их стороны и углы. Одно из основных свойств выпуклого шестиугольника – это равенство углов, то есть все его углы имеют одинаковую величину.
Определить существование выпуклого шестиугольника с равными углами можно, применив одно из свойств геометрии – сумма внутренних углов многоугольника. Для шестиугольника эта сумма составляет 720 градусов. Таким образом, чтобы выпуклый шестиугольник имел равные углы, каждый угол должен равняться 120 градусам.
Однако, в геометрии не существует выпуклого шестиугольника, все углы которого равны 120 градусам. При попытке построить такую фигуру возникает противоречие: сумма углов шестиугольника будет равняться 720 градусам, что несовместимо с равенством всех углов 120 градусам. Таким образом, выпуклый шестиугольник с равными углами не существует.
Понятие выпуклого шестиугольника

Шестиугольники могут быть невыпуклыми, когда хотя бы один из их углов является тупым или где-то нашлось два угла, сумма которых больше 180 градусов. Невыпуклые шестиугольники имеют "вогнутые" углы и части фигуры.
Выпуклые шестиугольники часто встречаются в природе и в архитектуре. Например, медоносные соты у пчел имеют форму регулярного выпуклого шестиугольника, так как такая форма обеспечивает наибольшую плотность покрытия площади при минимальном расходе материала.
| Свойства выпуклого шестиугольника: |
|---|
| Все углы шестиугольника острые. |
| Сумма углов внутри шестиугольника равна 720 градусов. |
| Один угол настоящего выпуклого шестиугольника не может быть больше 120 градусов. |
| Диагонали шестиугольника не пересекаются вне его границ. |
| Выпуклый шестиугольник имеет шесть сторон и шесть углов. |
Выпуклые шестиугольники имеют множество свойств, которые позволяют рассчитать их площадь, периметр, радиус вписанной и описанной окружности и другие геометрические параметры.
Важно отметить, что все углы выпуклого шестиугольника не обязаны быть равными. Однако, в определенных случаях, могут существовать выпуклые шестиугольники, у которых все углы равны. Такие шестиугольники называют равноугольными. Например, правильный шестиугольник, который является разновидностью равностороннего многоугольника, имеет все углы равными 120 градусам.
Если все углы выпуклого шестиугольника равны, то это значит, что из его сторон можно построить правильный шестиугольник.
Свойства выпуклого шестиугольника
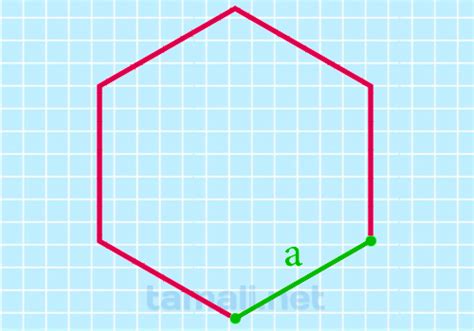
| Свойство | Описание |
|---|---|
| Углы | В выпуклом шестиугольнике все углы меньше 180 градусов. При суммировании всех углов получится 720 градусов. |
| Стороны | Все стороны выпуклого шестиугольника имеют одинаковую длину и параллельны друг другу. |
| Диагонали | Выпуклый шестиугольник имеет 9 диагоналей. Каждая диагональ соединяет два невертикально соседних угла и не пересекает другие диагонали. |
| Площадь | Площадь выпуклого шестиугольника можно вычислить, разделив его на треугольники и сложив площади каждого треугольника. |
| Периметр | Периметр выпуклого шестиугольника можно найти, сложив длины всех его сторон. |
Выпуклый шестиугольник с равными углами не существует, так как сумма всех углов должна быть равна 720 градусов, а для равных углов в шестиугольнике не выполняется это условие.
Описание
Шестиугольник, у которого все углы равны, называется правильным. Но правильный шестиугольник не может быть выпуклым,
потому что углы равны 120 градусам, что превышает 180 градусов и не удовлетворяет условиям выпуклости.
Таким образом, нет выпуклого шестиугольника с равными углами.
Доказательство невозможности шестиугольника с равными углами

Давайте рассмотрим вопрос о существовании выпуклого шестиугольника, у которого все углы равны. Предположим, что такой шестиугольник существует.
В выпуклом многоугольнике с n углами сумма внутренних углов равна (n-2)*180°. Таким образом, в шестиугольнике с равными углами сумма всех углов будет равна 720°.
Поскольку все углы в шестиугольнике равны, каждый угол будет равен 720° / 6 = 120°.
Но мы знаем, что в равностороннем треугольнике все углы равны 60°. Рассмотрим треугольник ABC с углами A, B и C, равными 120°:
| Угол | Значение |
|---|---|
| ∠A | 120° |
| ∠B | 120° |
| ∠C | 120° |
Мы видим, что сумма углов в треугольнике ABC равна 360°, что меньше 720°, необходимого для шестиугольника с равными углами.
Противоречие суммы углов в шестиугольнике

Вспомним, что сумма углов в выпуклом многоугольнике равна 180°. Из этого следует, что сумма всех углов в шестиугольнике должна равняться 720° (6 углов * 180°/угол).
Однако, если все углы шестиугольника равны, то каждый угол будет равняться 720°/6 = 120°. И сумма углов шестиугольника будет равна 6 углов * 120°/угол = 720°.
Таким образом, имеем противоречие: сумма углов в шестиугольнике, где все углы равны, равна и 720°, и 720°/6.
Это противоречие показывает, что не существует выпуклого шестиугольника, у которого все углы будут равны.
Анализ

Для решения данной задачи, необходимо проанализировать условие и определить, существует ли такой шестиугольник.
Известно, что углы выпуклого шестиугольника в сумме равны 720 градусов. Если все углы равны, то это значит, что каждый угол должен быть равен 720 / 6 = 120 градусам.
Однако, существует правило, согласно которому в выпуклом многоугольнике не может быть углов больше 180 градусов. Если угол в шестиугольнике равен 120 градусам, то сумма углов составит 6 * 120 = 720 градусов, что превышает 180 градусов.
Таким образом, выпуклый шестиугольник с равными углами невозможен.
Использование теоремы о сумме углов в многоугольнике
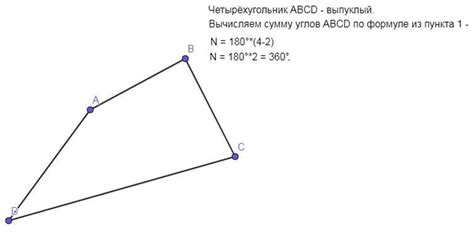
Эта теорема может быть использована для определения, существует ли выпуклый шестиугольник с равными углами. Если внутренние углы шестиугольника равны между собой, то сумма всех этих углов должна быть равна 720° (6 - 2) * 180°. Таким образом, если сумма всех углов шестиугольника не равна 720°, то такой шестиугольник не может считаться выпуклым.
При решении данной задачи можно воспользоваться геометрической формулой для вычисления суммы углов в многоугольнике. В случае шестиугольника это будет следующая формула: сумма углов = (6 - 2) * 180° = 720°.
Используя теорему о сумме углов в многоугольнике, можно определить, существует ли выпуклый шестиугольник с равными углами или нет.
Другие подходы к доказательству

Кроме метода противоречия, который был описан в предыдущем разделе, существуют и другие подходы к доказательству невозможности существования выпуклого шестиугольника с равными углами.
Один из них основан на теории меры. Согласно этой теории, выпуклый шестиугольник с равными углами должен иметь равные стороны. Но чтобы получить равные стороны, необходимо, чтобы углы и длины сторон шестиугольника были связаны некоторым определенным образом. Однако, при попытке найти такое соотношение, мы приходим к противоречию, и, следовательно, существование такого шестиугольника невозможно.
Другой подход основан на геометрических свойствах выпуклых шестиугольников. Если бы существовал выпуклый шестиугольник с равными углами, то все его диагонали были бы равными. Но при попытке построить такой шестиугольник и его диагонали, мы сталкиваемся с ограничениями геометрии и опять приходим к противоречию.
Таким образом, все эти подходы подтверждают, что выпуклый шестиугольник с равными углами не может существовать. Этот факт является важным результатом геометрии и имеет большое значение в различных областях науки и техники.
Отсутствие выпуклого шестиугольника с равными углами
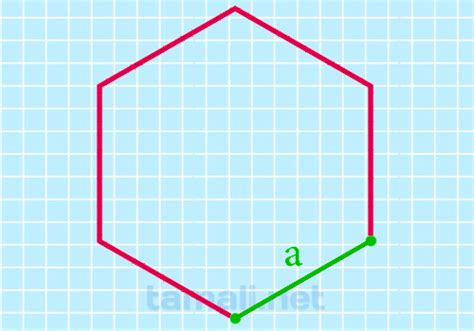
В геометрии существуют различные типы многоугольников, но не все из них могут иметь равные углы. В случае с шестиугольником, не существует выпуклого шестиугольника, у которого все углы были бы равными. Это можно объяснить следующими фактами:
1. Сумма внутренних углов шестиугольника всегда равна 720 градусам. Если бы все его углы были равными, каждый угол был бы равен 120 градусам. Тогда сумма углов получилась бы равной 720 градусам. Однако, выпуклый шестиугольник не может иметь 720 градусов, так как его углы ограничены значением меньше 180 градусов.
2. Допустим, что углы выпуклого шестиугольника равны и равны 120 градусам. Рассмотрим теперь одну его сторону и углы, которые образуются на его концах с соседними сторонами. Если все углы равны, значит, оба угла по ту и другую сторону от вершины также 120 градусов. Однако, в этом случае сумма углов будет больше 180 градусов, что невозможно для выпуклого шестиугольника.
Таким образом, выпуклый шестиугольник с равными углами не может существовать. Это свойство делает его особенным и позволяет геометрам исследовать другие типы многоугольников с разными углами и сторонами.



