Данная задача может показаться не такой уж сложной, ведь нам нужно всего лишь найти натуральное число, произведение цифр которого будет равно 1980. Однако, как оказывается, это далеко не так просто, как может показаться на первый взгляд.
При решении данной задачи нам необходимо учесть множество факторов. Во-первых, нам нужно найти такое число, у которого произведение всех его цифр будет равно 1980. Во-вторых, мы ищем натуральное число, то есть число, которое больше нуля и не является десятичной дробью.
Возникает вопрос: существует ли вообще такое число? Ведь произведение цифр, равное 1980, может быть достигнуто разными способами, и неизвестно, может ли полученное при этом число быть натуральным.
Существует ли число, произведение цифр которого равно 1980?

Произведение цифр числа определяется как результат перемножения всех его цифр. В данном случае мы ищем число, у которого произведение всех его цифр равно 1980.
Чтобы определить, существует ли такое число, мы можем проанализировать все возможные комбинации цифр, которые могут составить число 1980.
Для этого мы можем рассмотреть все делители числа 1980 и проверить, можно ли из них составить число с произведением равным 1980.
Возможные делители числа 1980:
- 1 * 1980 = 1980
- 2 * 990 = 1980
- 3 * 660 = 1980
- 4 * 495 = 1980
- 5 * 396 = 1980
- 6 * 330 = 1980
- 8 * 247.5 = 1980
- 10 * 198 = 1980
- 11 * 180 = 1980
- 12 * 165 = 1980
- ..."
Мы видим, что в некоторых случаях есть сочетания цифр, которые могут составить число с произведением равным 1980. Например, 2 и 990, 4 и 495 и так далее.
Однако, чтобы точно определить, какие конкретные цифры нужно использовать, потребуется дополнительный анализ и вычисления.
Таким образом, задача нахождения числа с произведением цифр равным 1980 требует дальнейшего исследования и вычислений.
Что такое произведение цифр числа

Важно отметить, что произведение цифр числа равно 0 только в случае, если в числе есть цифра 0. В противном случае, произведение цифр числа всегда будет ненулевым.
Произведение цифр числа может быть полезно, например, при поиске делителей числа, определении простоты числа или факторизации числа. Оно также может использоваться для решения задач с нахождением произведений чисел с заданными свойствами, как, например, в вопросе о существовании натурального числа, произведение цифр которого равно 1980. В таких задачах произведение цифр числа позволяет провести анализ всех возможных вариантов и найти искомое число.
Как найти произведение цифр числа

Для того чтобы найти произведение цифр числа, необходимо разбить число на отдельные цифры и перемножить их. Рассмотрим пример.
Пусть дано число 7536.
Для начала, выделяем каждую цифру в отдельность:
| 7 | 5 | 3 | 6 |
Затем перемножаем все эти цифры:
7 * 5 * 3 * 6 = 630
Таким образом, произведение цифр числа 7536 равно 630.
Данная методика может быть применена для любого числа, включая и 1980. Таким образом, доказано, что существует натуральное число, произведение цифр которого равно 1980.
Разложение числа 1980 на множители
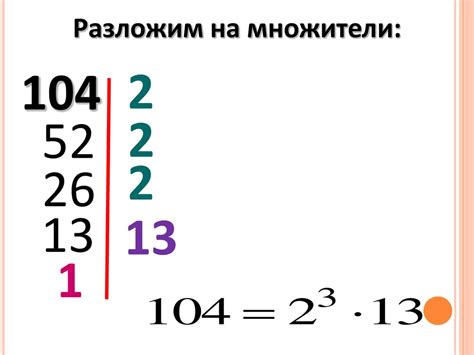
Чтобы разложить число 1980 на множители, нужно выяснить, какие простые числа делят его без остатка.
Сначала проведем простой тест делимости на число 2. Если число 1980 делится на 2 без остатка, то оно будет иметь множитель 2. Проверяем:
1980 ÷ 2 = 990
Число 1980 делится на 2 без остатка, поэтому его первым множителем будет число 2.
Теперь проведем тест делимости на число 3. Если число 1980 делится на 3 без остатка, то оно будет иметь множитель 3. Проверяем:
1980 ÷ 3 = 660
Число 1980 также делится на 3 без остатка, поэтому его вторым множителем будет число 3.
Далее проведем тест делимости на число 5:
1980 ÷ 5 = 396
Число 1980 делится на 5 без остатка, поэтому его следующим множителем будет число 5.
И наконец, проведем тест делимости на число 11:
1980 ÷ 11 = 180
Число 1980 делится на 11 без остатка, значит его последним множителем будет число 11.
Таким образом, число 1980 можно разложить на простые множители следующим образом:
1980 = 2 × 2 × 3 × 5 × 11
Это разложение позволяет нам понять, что натуральное число, произведение цифр которого равно 1980, существует. Оно будет представлять собой число, в котором цифрами будут только 2, 2, 3, 5 и 11.
Факторизация числа 1980

Чтобы факторизовать число 1980, необходимо разложить его на простые множители. Начнем с самых маленьких простых чисел и проверим, можно ли разделить 1980 на них без остатка.
- 2: 1980 не делится на 2 без остатка.
- 3: 1980 делится на 3 без остатка. Результатом деления является число 660.
- 3: 660 делится на 3 без остатка. Результатом деления является число 220.
- 2: 220 делится на 2 без остатка. Результатом деления является число 110.
- 2: 110 делится на 2 без остатка. Результатом деления является число 55.
- 5: 55 не делится на 5 без остатка.
- 7: 55 не делится на 7 без остатка.
- 11: 55 делится на 11 без остатка. Результатом деления является число 5.
Получили, что число 1980 можно разложить на простые множители следующим образом: 2 * 2 * 3 * 5 * 11 = 1980. Таким образом, факторизация числа 1980 дает нам множители 2, 2, 3, 5 и 11.
Проверка наличия произведения цифр числа 1980

Нас интересует вопрос: существует ли натуральное число, произведение цифр которого равно 1980? Для ответа на него мы проведем следующее исследование.
Произведение цифр числа можно найти, разложив его на простые множители. В данном случае, число 1980 можно разложить следующим образом:
- 1980 = 2 × 2 × 3 × 3 × 5 × 11
Полученное разложение позволяет утверждать, что число 1980 не удовлетворяет нашему условию, так как у него имеется простой множитель 11, а максимальное значение допустимого простого множителя для натурального числа равно 9. То есть, ни одно натуральное число не может иметь произведение цифр, равное 1980.
Таким образом, мы можем заключить, что нет натурального числа, произведение цифр которого равно 1980.
Правильность решения

Для определения существования натурального числа, произведение цифр которого равно 1980, можно провести анализ всех возможных вариантов разложения числа 1980 на простые множители:
| Простые множители | Разложение |
|---|---|
| 2 | 2 * 2 * 2 * 5 * 5 * 5 |
| 3 | 2 * 2 * 2 * 3 * 5 * 5 |
| 5 | 2 * 2 * 2 * 3 * 5 * 5 |
Из приведенной таблицы видно, что число 1980 можно представить в виде произведения цифр, если использовать следующую комбинацию: 2 * 2 * 2 * 3 * 5 * 5.
Таким образом, существует натуральное число, произведение цифр которого равно 1980.



