Треугольник – это одна из базовых геометрических фигур, определяемая тремя сторонами и тремя углами. Проверить, является ли треугольник прямоугольным по сторонам, может оказаться полезным для решения разнообразных задач. Для этого нужно воспользоваться одним из известных треугольных неравенств и выполнить несложные вычисления.
Метод проверки треугольника на прямоугольность по сторонам включает в себя несколько простых шагов. В первую очередь, необходимо измерить длины всех трех сторон треугольника. Затем, обозначим наибольшую сторону через c, а две оставшиеся стороны – через a и b. Возможны три случая: если c2 равно a2 + b2, то треугольник является прямоугольным; если c2 больше, то треугольник – тупоугольный; если c2 меньше, то треугольник – остроугольный.
Проверка треугольника на прямоугольность по сторонам может быть полезна в решении задач из различных областей – от геометрии до строительства. Знание, является ли треугольник прямоугольным, позволяет определить, какие дополнительные свойства и формулы могут быть применены, чтобы найти другие неизвестные величины, такие как углы или стороны треугольника. Это особенно важно при решении задач на построение треугольников и нахождение неизвестных длин сторон.
Что такое проверка треугольника на прямоугольность?

Треугольник может быть прямоугольным, если выполнено следующее условие, известное как теорема Пифагора:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, если длины сторон треугольника удовлетворяют этому условию, то треугольник является прямоугольным.
Для проверки треугольника на прямоугольность необходимо знать длины его сторон. Для этого можно воспользоваться теоремой косинусов или теоремой синусов. При нахождении длин сторон треугольника можно применить теорему Пифагора и проверить выполнение условия для прямоугольного треугольника.
Умение проверять треугольник на прямоугольность полезно при решении различных геометрических задач, например, при нахождении высоты, медианы или биссектрисы треугольника.
Зачем нужно проверять треугольник на прямоугольность?

Одним из основных преимуществ прямоугольного треугольника является наличие точек симметрии, которые существенно упрощают решение математических задач и позволяют применять специальные правила.
Прямоугольные треугольники применяются во многих областях, таких как архитектура, инженерия, физика, геодезия, астрономия и даже искусство. Использование прямоугольных треугольников позволяет нам измерять расстояния, рассчитывать площади, определять направления и многое другое.
Кроме того, знание принципов и формул, связанных с прямоугольными треугольниками, может быть полезным не только в профессиональной деятельности, но и в повседневной жизни. Например, при выборе места для строительства, измерении площади участка земли или создании дизайна интерьера.
Проверка треугольника на прямоугольность позволяет нам более точно понимать и визуализировать фигуры, а также использовать математические методы для решения практических задач. Поэтому изучение и понимание принципов прямоугольных треугольников является неотъемлемой частью математического образования и практического применения математики в нашей жизни.
Методы проверки

Существует несколько методов для проверки треугольника на прямоугольность по сторонам. Вот некоторые из них:
| Метод | Описание |
|---|---|
| Теорема Пифагора | Проверка выполнения теоремы Пифагора, где квадрат гипотенузы равен сумме квадратов катетов. |
| Сравнение квадратов сторон | Сравнение квадратов сторон треугольника следующим образом: если сумма квадратов двух меньших сторон равна квадрату большей стороны, то треугольник прямоугольный. |
| Угловые отношения | Использование угловых отношений (тангенс, синус, косинус) для определения прямого угла между сторонами треугольника. |
Выбор метода зависит от конкретной задачи и имеющихся данных. Некоторые методы могут быть более точными или удобными в определенных ситуациях.
Проверка треугольника на прямоугольность с использованием теоремы Пифагора
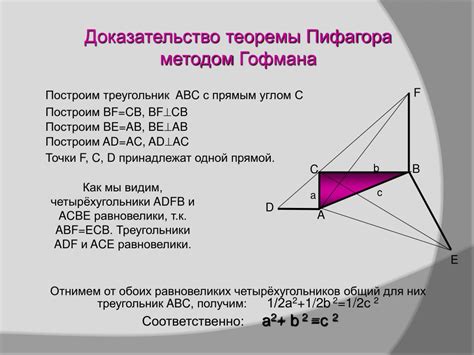
Для проверки треугольника на прямоугольность с использованием теоремы Пифагора необходимо измерить длины всех трех сторон треугольника. Затем, используя измеренные значения, провести следующие расчеты:
1. Возвести в квадрат длины каждой стороны треугольника.
a^2 = длина_стороны_a * длина_стороны_a b^2 = длина_стороны_b * длина_стороны_b c^2 = длина_стороны_c * длина_стороны_c2. Просуммировать квадраты длин двух катетов.
сумма_квадратов_катетов = a^2 + b^23. Сравнить полученное значение с квадратом длины гипотенузы.
если сумма_квадратов_катетов == c^2, то треугольник прямоугольный иначе треугольник не является прямоугольнымЕсли сумма квадратов длин двух катетов равна квадрату длины гипотенузы, то треугольник является прямоугольным, в противном случае треугольник не является прямоугольным.
Таким образом, использование теоремы Пифагора позволяет проверить треугольник на прямоугольность, основываясь на измеренных значениях его сторон.
Проверка треугольника на прямоугольность с использованием углов
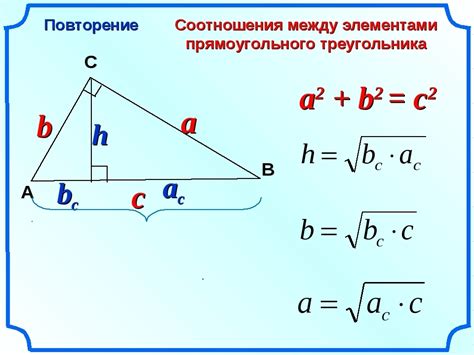
Для определения прямоугольности треугольника можно использовать информацию о его углах. Если в треугольнике есть прямой угол, то он называется прямоугольным. Прямой угол равен 90 градусам.
Для проверки треугольника на прямоугольность с использованием углов необходимо знать значения всех трех углов треугольника. Если один из углов равен 90 градусам, то треугольник является прямоугольным.
Чтобы найти значения углов треугольника, можно использовать формулу:
Сумма углов треугольника равна 180 градусам: угол1 + угол2 + угол3 = 180.
Итак, если один из углов равен 90 градусам, то треугольник прямоугольный, если нет - треугольник не прямоугольный.
Однако, для полной проверки на прямоугольность треугольника необходимо также учесть длины его сторон.
Сочетание информации о длинах сторон треугольника и его углов поможет более точно определить, является ли треугольник прямоугольным или нет.
Как провести проверку?

Теорема Пифагора гласит, что для прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов:
c2 = a2 + b2
Для проведения проверки, нужно знать длины всех сторон треугольника: гипотенузу и два катета. Затем можно подставить значения в формулу и проверить, будет ли равенство выполняться.
Если равенство выполняется, то треугольник является прямоугольным. Если неравенство выполняется, то треугольник не является прямоугольным.
Важно помнить, что для проведения проверки нужно убедиться, что стороны треугольника соответствуют условиям прямоугольного треугольника и корректно измерены.
Примеры проверки треугольника на прямоугольность с использованием теоремы Пифагора
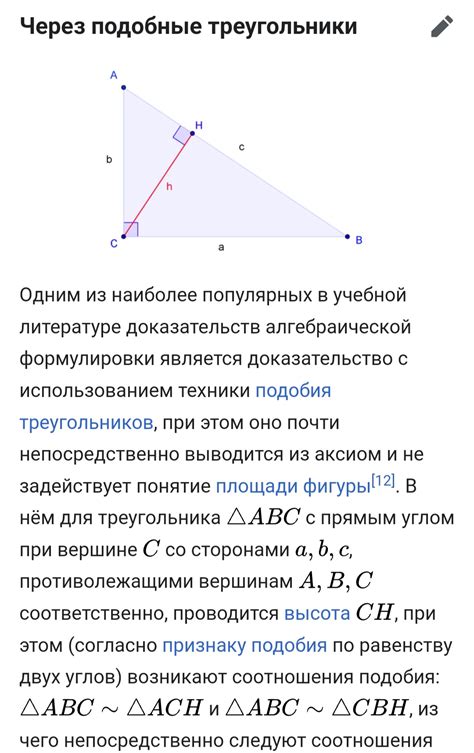
Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применим эту теорему для проверки треугольника на прямоугольность. Рассмотрим несколько примеров:
Пример 1:
Заданы стороны треугольника: a = 3, b = 4, c = 5.
Проверим выполнение теоремы Пифагора:
a2 + b2 = 32 + 42 = 9 + 16 = 25
c2 = 52 = 25
Сумма квадратов катетов равна квадрату гипотенузы. Треугольник является прямоугольным.
Пример 2:
Заданы стороны треугольника: a = 5, b = 12, c = 13.
Проверим выполнение теоремы Пифагора:
a2 + b2 = 52 + 122 = 25 + 144 = 169
c2 = 132 = 169
Сумма квадратов катетов равна квадрату гипотенузы. Треугольник является прямоугольным.
Пример 3:
Заданы стороны треугольника: a = 7, b = 8, c = 10.
Проверим выполнение теоремы Пифагора:
a2 + b2 = 72 + 82 = 49 + 64 = 113
c2 = 102 = 100
Сумма квадратов катетов не равна квадрату гипотенузы. Треугольник не является прямоугольным.
Таким образом, используя теорему Пифагора, мы можем проверять треугольники на прямоугольность, основываясь на значениях их сторон.
Примеры проверки треугольника на прямоугольность с использованием углов

Существует несколько способов проверки треугольника на прямоугольность с использованием углов:
- Метод 1: Использование теоремы Пифагора
- Метод 2: Использование таблицы значений функции тангенс
- Метод 3: Использование косинуса угла
- Метод 4: Использование синуса угла
Если сумма квадратов двух меньших углов треугольника равна квадрату наибольшего угла, то треугольник является прямоугольным. Например, если углы треугольника равны 30°, 60° и 90°, то треугольник будет прямоугольным.
Если тангенс одного из углов треугольника равен отношению двух других сторон треугольника, то треугольник является прямоугольным. Например, если углы треугольника равны 45°, 45° и 90°, то треугольник будет прямоугольным.
Если косинус одного из углов треугольника равен нулю, то треугольник является прямоугольным. Например, если углы треугольника равны 0°, 90° и 90°, то треугольник будет прямоугольным.
Если синус одного из углов треугольника равен единице или нулю, то треугольник является прямоугольным. Например, если углы треугольника равны 30°, 60° и 90°, то треугольник будет прямоугольным.
При проверке треугольника на прямоугольность с использованием углов необходимо помнить, что углы треугольника всегда суммируются к 180°.



