В математике простое число - это число, которое имеет только два делителя: единицу и само себя. Они играют важную роль в различных областях, таких как шифрование, криптография и теория чисел. Однако, иногда требуется быстро определить, является ли число простым или нет, без использования сложных алгоритмов и методов.
Простой алгоритм проверки на простоту основан на простой идее: проверить все числа от 2 до корня из данного числа и убедиться, что они не являются делителями этого числа. Если в процессе проверки ни одно из чисел не является делителем, то число считается простым.
Этот алгоритм эффективен для небольших чисел, но может быть медленным для больших чисел. Однако, для большинства практических применений он может быть достаточно быстрым и эффективным.
Если вы хотите узнать, является ли число простым или нет, вы можете использовать простой алгоритм проверки на простоту. Просто проверьте все числа от 2 до корня из данного числа и убедитесь, что ни одно из них не является делителем. Если ни одно число не делит данное число без остатка, то оно является простым.
Как определить простое число: простой алгоритм

Существует много различных алгоритмов для проверки простоты чисел, однако простой алгоритм наиболее понятен и прост в реализации. Он заключается в проверке делителей числа исключительно до квадратного корня этого числа. Если у числа есть делитель в этом диапазоне, то оно не является простым. Если делителя не найдено, то число является простым.
В данном простом алгоритме нет необходимости проверять делители после квадратного корня числа, потому что если число делится на какое-либо число больше его квадратного корня, то должно также делиться и на меньшее число.
Используя этот простой алгоритм, можно легко проверить простоту любого числа и использовать эту информацию в различных задачах, связанных с числами и численными операциями.
Алгоритм определения простого числа
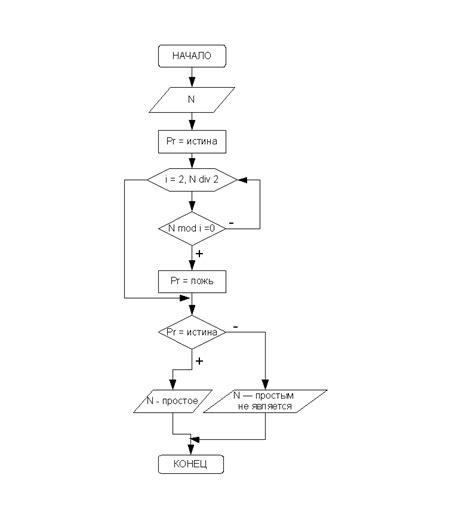
Для определения, является ли число простым или нет, можно воспользоваться простым алгоритмом:
- Начать с проверки числа на делимость на все числа, начиная с 2 и заканчивая числом, меньшим, чем само число.
- Если число делится на любое из этих чисел без остатка, то оно не является простым, и алгоритм завершается.
- Если число не делится ни на одно из этих чисел без остатка, оно является простым.
Например, чтобы проверить, является ли число 13 простым, необходимо проверить его на делимость на все числа от 2 до 12. В данном случае, число 13 не делится ни на одно из этих чисел, поэтому оно является простым.
Алгоритм определения простого числа позволяет эффективно определить, является ли число простым или нет. Однако с увеличением числа, время выполнения алгоритма также увеличивается, что делает его не самым эффективным для больших чисел.



