График функции y=3x - один из самых простых и часто используемых в математике. Он представляет собой прямую линию на координатной плоскости, проходящую через начало координат. Эта функция имеет вид y=kx, где k - коэффициент пропорциональности, в данном случае равный 3.
Если мы зададим любое значение для переменной x и вычислим значение y, то получим точку (x, y), которая будет лежать на графике функции. Таким образом, график функции y=3x является множеством всех точек, удовлетворяющих данному уравнению.
Можно ли утверждать, что любая точка на плоскости принадлежит графику функции y=3x? Ответ на этот вопрос зависит от значения координат данной точки.
Определение графика функции
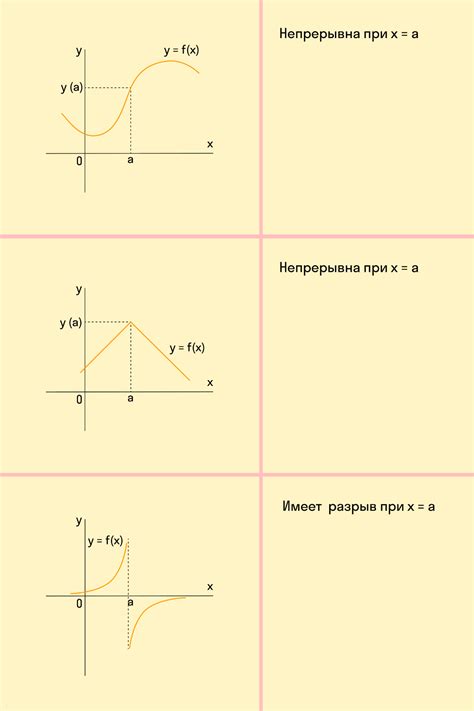
График функции можно представить в виде изображения на плоскости, где ось абсцисс отображает значения аргумента функции, а ось ординат - значения самой функции.
При построении графика функции необходимо знать значение функции для различных значений аргумента. Чтобы найти точки, которые лежат на графике функции, можно подставлять различные значения аргумента в функцию и вычислять соответствующее значение функции.
На графике функции можно определить такие важные характеристики, как: экстремумы, возрастание и убывание функции, пересечение графика с осями координат, промежутки монотонности и выпуклости/вогнутости.
Формула функции y=3x

Формула функции y=3x представляет собой линейную функцию, где значение y равно утроенному значению x. Другими словами, каждое значение y равно трем разам значения x.
Функция y=3x можно представить в виде таблицы, где каждому значению x сопоставлено соответствующее значение y. Ниже приведена таблица значений:
| x | y=3x |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
График функции y=3x - прямая линия, проходящая через начало координат и имеющая положительный наклон. Каждая точка на этой линии соответствует значению из таблицы.
Таким образом, график функции y=3x и соответствующая ей таблица значений подтверждают, что функция y=3x принадлежит графику данной функции.
Какова природа графика функции
Природа графика функции зависит от свойств самой функции. Например, для линейной функции, такой как y=3x, график будет прямой линией, проходящей через начало координат. С увеличением значения x, значение y также увеличивается в три раза.
Важно отметить, что график функции может иметь различные формы, в зависимости от типа функции. Например, функция вида y=x^2 будет иметь параболическую форму графика, функция вида y=sin(x) будет иметь волнообразную форму, а функция вида y=exp(x) будет иметь стремительно возрастающую кривую.
Анализ графика функции позволяет определить основные характеристики функции, такие как область определения, область значений, монотонность, периодичность и точки перегиба. Благодаря графику функции можно лучше понять ее свойства и использовать эту информацию в решении задач и вычислениях.
Способы определения принадлежности графика функции
| Способ определения | Описание |
|---|---|
| Изучение явных математических выражений | Анализ выражений, определяющих функцию, для проверки соответствия заданным значениям |
| Анализ свойств функции | Изучение свойств функции и её графика, сравнение с характерными признаками |
| Графический метод | Построение графика функции и его сравнение с графиками других функций |
Как определить точку на графике функции
Для того чтобы определить точку на графике функции, необходимо знать значения аргумента (x) и соответствующего значения функции (y).
Процесс определения точки на графике функции можно разделить на несколько шагов:
- Находим значение аргумента (x), которое требуется проверить.
- Подставляем найденное значение аргумента (x) в уравнение функции, получаем значение функции (y).
- Полученное значение функции (y) является ординатой (высотой) соответствующего графика в заданной точке.
Например, рассмотрим функцию y = 3x. Чтобы определить точку на ее графике, можно выбрать значение аргумента (x), например, x = 2, и подставить его в уравнение функции:
| x | y = 3x |
|---|---|
| 2 | 6 |
Таким образом, при x = 2, соответствующая точка на графике функции y = 3x будет иметь координаты (2, 6).
Аналогично можно определить точки на графике любой другой функции, зная значения аргумента и функции в этих точках.
Ответы на вопросы о принадлежности графика функции y=3x
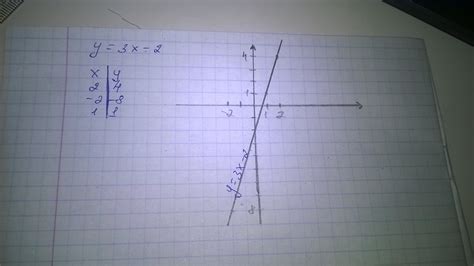
Ниже представлены ответы на наиболее распространенные вопросы о принадлежности графика функции y=3x:
- Принадлежит ли график функции y=3x кривой?
График функции y=3x – это прямая линия, так как уравнение имеет степень 1. Прямая линия не является кривой, она представляет собой линейную зависимость между x и y. - Как отобразить график функции y=3x на координатной плоскости?
Для отображения графика функции y=3x на координатной плоскости необходимо провести прямую линию, проходящую через начало координат (0,0) и имеющую угловой коэффициент 3. Это может быть выполнено при помощи проведения двух точек на прямой и их последующего соединения. - Как определить точку пересечения графика функции y=3x с осями координат?
Для определения точек пересечения графика функции y=3x с осями координат необходимо приравнять y или x к нулю и решить полученное уравнение. В данном случае, для нахождения точки пересечения с осью y, y необходимо приравнять к нулю: 3x = 0 → x = 0. Таким образом, график функции y=3x пересекает ось y в точке (0,0). Аналогичным образом можно найти точку пересечения с осью x, приравняв x к нулю. - Является ли график функции y=3x возрастающей или убывающей?
График функции y=3x является возрастающей прямой. Это значит, что с увеличением значения x, значение y также увеличивается. Значение углового коэффициента функции, равное 3, указывает на то, что график функции будет иметь положительный наклон.
Изучение графика функции y=3x позволяет лучше понять ее свойства и взаимосвязь между значениями x и y. Это важно при анализе различных задач и применении функции в реальных ситуациях.
Ответы на вопросы о природе графика функции y=3x
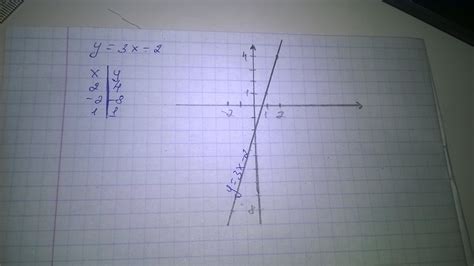
Когда рассматриваем график функции y=3x, возникают вопросы о его природе и свойствах. Ниже приведены ответы на некоторые из них:
Каков характер этого графика?
График функции y=3x представляет собой прямую линию, проходящую через начало координат (0,0) и имеющую угол наклона 45° к положительному направлению оси x.
Какова область определения и значения функции?
Функция y=3x определена для всех действительных чисел x. Значение функции (y) будет зависеть от значения аргумента (x) и будет равно трём умноженным на это значение аргумента.
Какова симметрия графика?
График функции y=3x обладает осями симметрии. Он симметричен относительно оси x (вертикальной оси) и оси y (горизонтальной оси). Это означает, что если (x, y) является точкой на графике, то точки (-x, y), (x, -y) и (-x, -y) также будут находиться на этом графике.
Как изменяется график при изменении значения коэффициента 3?
Увеличение коэффициента 3 будет приводить к более крутому наклону прямой, а уменьшение этого коэффициента - к менее крутому наклону. Например, если коэффициент равен 1, то график будет обычной прямой с наклоном 45°, как у функции y=x.
Эти ответы помогут вам лучше понять природу графика функции y=3x и его основные свойства.



