Симметричность области определения функции является важным свойством, которое позволяет понять, каким образом меняется функция относительно оси симметрии. Она позволяет предсказать поведение функции и найти особые точки, такие как экстремумы или точки перегиба.
Для определения симметричности области определения функции необходимо анализировать ее график и выявлять наличие определенных осей симметрии. Одной из наиболее распространенных осей симметрии является ось ординат, прямая, проходящая через вершину функции. Если функция является симметричной относительно этой оси, то при замене аргумента на противоположное значение, значение функции также меняется на противоположное.
Однако, симметрия может иметь и другие формы. Например, функция может быть симметричной относительно оси абсцисс или иметь центральную симметрию, когда она симметрична относительно точки. Для определения этих видов симметрии необходимо провести аналогичные исследования графика функции.
Что такое симметричность области определения функции?

Другими словами, если функция определена на интервале [-a, a], то график функции будет симметричен относительно вертикальной оси x=0. Если функция определена на интервале (-a, a), то график функции будет симметричен как относительно вертикальной оси x=0, так и относительно точки x=0.
Симметрия области определения может быть различных видов: симметрия относительно оси, симметрия относительно точки или симметрия относительно линии.
Симметрия области определения функции имеет важное значение при изучении ее свойств и характеристик. Она позволяет сделать определенные утверждения о значении функции на основе информации о ее значении на симметричных точках или областях.
Например, если функция четная, то она будет иметь симметричную область определения относительно оси и значением функции в точке x будет равно значению функции в точке -x. Если функция нечетная, то она также будет иметь симметричную область определения относительно точки и значение функции в точке x будет равно значению функции в точке -x с противоположным знаком.
Симметрия области определения функции является одним из важных свойств, которые помогают нам лучше понять ее поведение и свойства при решении математических задач и проблем.
Симметричность области определения функции – что это значит?

Область определения функции – это множество всех значений x, для которых функция имеет смысл. Если функция определена на всей числовой прямой, то ее область определения – это множество всех действительных чисел.
Если функция симметрична относительно своей области определения, то значит, что для каждого значения x в области определения, функция имеет соответствующее значение f(x), и для каждого значения -x в области определения, функция также имеет значение f(-x), причем f(x) = f(-x).
Другими словами, функция симметрична относительно своей области определения, если ее график сохраняет свою форму относительно оси симметрии, которая проходит через начало координат.
Рассмотрим пример функции f(x) = x^2. Область определения этой функции состоит из всех действительных чисел. Если мы построим график этой функции на координатной плоскости, то увидим, что он является симметричным относительно оси y.
| x | f(x) = x^2 |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Как видно из таблицы и графика функции f(x) = x^2, значения f(x) и f(-x) равны для любого значения x из области определения.
Таким образом, понимание симметричности области определения функции поможет нам лучше понять свойства и характеристики функций, а также использовать их в различных математических и научных приложениях.
Симметричность области определения функции и ее график
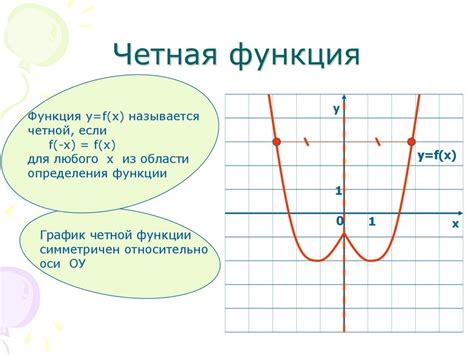
Симметричность области определения функции может быть разделена на несколько типов:
- Симметричность относительно оси y. Если для функции f(x) выполняется условие f(x) = f(-x) для любого значения x в области определения, то область определения функции симметрична относительно оси y.
- Симметричность относительно начала координат. Если для функции f(x) выполняется условие f(x) = -f(-x) для любого значения x в области определения, то область определения функции симметрична относительно начала координат.
- Симметричность относительно оси x. Если для функции f(x) выполняется условие f(x) = -f(x) для любого значения x в области определения, то область определения функции симметрична относительно оси x.
Понимание симметрии области определения функции может быть важным при анализе графика функции. Например, при изучении симметричности относительно оси y, мы можем найти точки симметрии и узнать больше о поведении функции в разных частях области определения.
Таким образом, исследование симметрии области определения функции и ее графика может помочь нам лучше понять структуру функции и ее особенности. Это важный аспект в изучении функций и их графиков в математике.
Примеры симметричной области определения функции

Симметричность области определения функции означает, что функция обладает особенной структурой, где значения функции симметрично распределены относительно некоторой оси или точки. В таких случаях, функция может иметь определенные свойства, которые делают ее более простой для анализа и понимания. Рассмотрим некоторые примеры симметричной области определения функции.
1. Четная функция: Функция называется четной, если ее значение сохраняется при смене знака аргумента. Одним из примеров четной функции является функция косинуса (cos(x)). Область определения функции косинуса - все действительные числа, и график функции симметричен относительно оси ординат.
2. Нечетная функция: Функция называется нечетной, если ее значение меняется знак при смене знака аргумента. Примером нечетной функции является функция синуса (sin(x)). Область определения функции синуса также - все действительные числа, и график функции симметричен относительно начала координат.
3. Периодическая функция: Функция является периодической, если ее значения повторяются с определенным интервалом. Примером периодической функции является функция тангенса (tan(x)). Область определения функции тангенса может быть ограничена в зависимости от значения бесконечности, но значения функции повторяются в рамках интервала.
4. Равноамплитудная функция: Функция называется равноамплитудной, если амплитуда значений функции симметрична относительно некоторой оси или точки. Примером равноамплитудной функции является функция модуля (|x|). Область определения функции модуля - все действительные числа, и график функции симметричен относительно оси ординат.
Все эти примеры симметричных областей определения функции имеют свои уникальные свойства и играют важную роль в математическом анализе и моделировании. Изучение симметричности области определения функции помогает понять ее особенности и использовать их в решении математических задач.
Что делать, если область определения функции не является симметричной?

В некоторых случаях область определения функции может быть несимметричной относительно оси или точки. Это может создать определенные сложности при анализе и графическом представлении функции. Однако, несимметричность области определения не означает, что функция не может быть изучена или использована.
Если область определения функции не является симметричной, следует учитывать особенности ее графика и анализировать его в соответствии с этими особенностями. Некоторые возможные действия, которые можно предпринять:
1. Изучение асимптот: Если функция имеет асимптоты, это может дать полезную информацию о ее поведении на бесконечности. Асимптоты могут помочь понять, как функция приближается к бесконечности и как она ведет себя вне области определения.
2. Анализ точек разрыва: Если функция имеет точки разрыва вне симметричной области определения, их нужно учитывать при анализе ее свойств. Эти точки могут влиять на график функции и обусловить его особенности.
3. Проверка свойств функции: Изучение свойств функции, таких как четность, нечетность или периодичность, может помочь в понимании ее поведения вне симметричной области определения. Эти свойства могут дать дополнительную информацию о графике функции и ее поведении.
Важно помнить, что несимметричность области определения не означает, что функция не может быть изучена или использована. Несмотря на несимметрию, ее график и свойства все равно могут быть анализированы и использованы при решении задач или нахождении оптимальных решений. Поэтому, если область определения функции не является симметричной, следует учитывать особенности ее графика и связать их с анализом и решением поставленных задач.



