Эквивалентность двух логических формул – это свойство, при котором две формулы выполняются одновременно на всех наборах значений переменных. В других словах, если результат выражения для первой и второй формулы всегда одинаковы для всех возможных значений переменных, то можно сказать, что данные формулы эквивалентны.
Существует несколько методов для определения эквивалентности двух логических формул:
- Алгебраический метод: использует правила алгебры логики для преобразования формул и поиска эквивалентных выражений.
- Таблица истинности: создается таблица, в которой перечислены все возможные значения переменных, а затем вычисляются значения формул. Если значения формул совпадают на всех строках таблицы, то формулы эквивалентны.
- Метод преобразования формул: применяется операции упрощения логических выражений и логические эквивалентности. Также применяются правила понижения уровня вложенности формул, логические эквивалентности и законы ассоциативности и дистрибутивности логических операций.
Процесс определения эквивалентности может быть сложным, особенно для сложных формул. Методы, такие как алгебраический метод или метод преобразования формул, могут значительно упростить этот процесс и помочь определить, являются ли две логические формулы эквивалентными.
Почему важно определить эквивалентность логических формул?

Знание, что две формулы эквивалентны, позволяет упростить и улучшить решение различных задач. Это может быть полезно при проверке правильности логических выражений, оптимизации логических схем, а также при поиске преобразований и упрощений логических формул.
Определение эквивалентности логических формул осуществляется с использованием различных методов. Важно понимать, что эти методы позволяют доказать эквивалентность или неэквивалентность формул, что имеет важное значение в различных областях, таких как математика, информатика, логика и теория вычислений.
В общем случае определение эквивалентности формул может быть нетривиальным заданием, требующим аккуратного анализа и использования логических законов и правил. Однако существуют и конкретные методы решения этой задачи для различных классов формул.
Поэтому умение определить эквивалентность логических формул является важным инструментом в решении задач, связанных с логикой и вычислительными процессами. Это позволяет улучшить эффективность решений, повысить точность результатов и избежать ошибок в логическом анализе.
Что такое эквивалентность двух логических формул?

Для определения эквивалентности двух логических формул используются различные методы и техники. Одним из основных методов является таблица истинности, которая позволяет анализировать все возможные значения переменных и устанавливать, совпадают или нет значения логических выражений при данных значениях переменных.
Другими методами определения эквивалентности формул являются алгебраические преобразования и законы логики. При помощи этих методов можно сокращать формулы, упрощать их, исключать повторяющиеся части и устанавливать их эквивалентность с помощью доказательств.
Примером эквивалентности двух логических формул может служить формула A ∧ (B ∨ C) и формула (A ∧ B) ∨ (A ∧ C), где ∧ – операция логического И (“и”), ∨ – операция логического ИЛИ (“или”). При проверке всех возможных комбинаций значений переменных A, B и C с помощью таблицы истинности можно убедиться, что обе формулы дают одинаковые результаты.
| A | B | C | A ∧ (B ∨ C) | (A ∧ B) ∨ (A ∧ C) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Методы определения эквивалентности

Один из таких методов - метод таблиц истинности. Суть метода заключается в построении таблицы истинности для обеих формул и сравнении полученных результатов. Если значения всех переменных в таблице истинности совпадают для обеих формул, то они эквивалентны. Однако этот метод является достаточно трудоемким и не всегда применим для сложных формул.
Другим методом определения эквивалентности является преобразование формул. С помощью логических законов и теорем можно преобразовывать формулы до равносильного вида. Если две формулы удалось привести к одному и тому же виду, то они эквивалентны. Этот метод часто применяется при доказательстве эквивалентности формул в математических и логических задачах.
Также существует метод Дэвиса-Патнема-Леммона, который основан на алгоритмах сведения формул к дизъюнктивной нормальной форме (ДНФ) и конъюнктивной нормальной форме (КНФ). Если формулы удалось привести к одной и той же ДНФ или КНФ, то они эквивалентны.
Наконец, существует метод проверки эквивалентности с использованием программного обеспечения. С помощью специальных программ можно задать две формулы и получить ответ о том, являются ли они эквивалентными или нет. Этот метод позволяет автоматизировать процесс проверки эквивалентности и упростить его для сложных формул.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Метод таблиц истинности | Точный результат, применим для простых формул | Трудоемкий, не применим для сложных формул |
| Метод преобразования формул | Метод аналитического решения, применим для математических задач | Требует знания логических законов и теорем |
| Метод Дэвиса-Патнема-Леммона | Приводит формулы к ДНФ или КНФ, применим для широкого класса формул | Трудоемкий, не всегда дает точный результат |
| Метод программного обеспечения | Автоматизация процесса, применим для сложных формул | Требуется специальное программное обеспечение |
Построение таблиц истинности
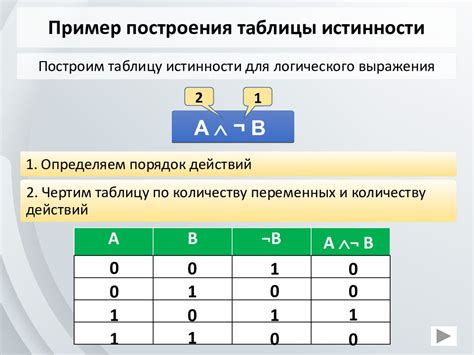
Для построения таблицы истинности необходимо знать количество различных значений, которые могут принимать входные переменные. Затем все возможные комбинации значений переменных упорядочиваются в столбцах таблицы, а значения логической формулы для каждой комбинации вычисляются и записываются в последующие столбцы.
Построение таблиц истинности выявляет также зависимости и закономерности в логических формулах. Это позволяет более глубоко понять и изучить структуру формулы и особенности ее работы.
Пример:
Рассмотрим, например, две логические формулы: "A и B" и "не (A или B)". Для построения таблицы истинности определяем количество различных значений переменных A и B - в данном случае это всего два значения: истина (1) и ложь (0).
| A | B | A и B | не (A или B) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Применение алгоритма эквивалентности

Процесс применения алгоритма эквивалентности обычно состоит из нескольких этапов. На первом этапе необходимо задать две логические формулы, которые требуется сравнить. Затем следует провести анализ формулы и определить ее структуру и логические операции, которые в ней присутствуют.
На втором этапе происходит непосредственное сравнение формул. Алгоритм обходит формулы и проверяет, эквивалентны ли они друг другу в соответствии с заданными правилами и условиями. Если формулы эквивалентны, алгоритм возвращает true; если формулы не эквивалентны, алгоритм возвращает false.
Для упрощения процесса применения алгоритма эквивалентности часто используется таблица истинности. Таблица истинности позволяет представить все возможные варианты значений переменных, входящих в формулу, и их логических сочетаний. Сравнивая значения формул для всех этих вариантов, можно определить их эквивалентность.
| Переменные | Значение 1 | Значение 2 | Формула 1 | Формула 2 | Результат |
|---|---|---|---|---|---|
| A | true | true | true | true | Эквивалентны |
| A | true | false | true | false | Не эквивалентны |
| A | false | true | false | true | Не эквивалентны |
| A | false | false | false | false | Эквивалентны |
Таким образом, применение алгоритма эквивалентности позволяет установить, равны ли две логические формулы друг другу. Это особенно полезно в задачах проверки правильности программ, оптимизации кода и доказательства теорем в математике и логике.
Примеры определения эквивалентности

Пример 1:
| Формула A | Формула B | Эквивалентность |
|---|---|---|
| A ∧ B | B ∧ A | Да |
| A ∨ B | B ∨ A | Да |
| A → B | ¬A ∨ B | Да |
Пример 2:
| Формула A | Формула B | Эквивалентность |
|---|---|---|
| A ∧ (B ∨ C) | (A ∧ B) ∨ (A ∧ C) | Да |
| A ∨ (B ∧ C) | (A ∨ B) ∧ (A ∨ C) | Да |
| A ∧ (B → C) | (A ∧ B) → (A ∧ C) | Нет |
Пример 3:
| Формула A | Формула B | Эквивалентность |
|---|---|---|
| A ∨ (B ∨ C) | (A ∨ B) ∨ C | Да |
| A ∧ (B ∧ C) | (A ∧ B) ∧ C | Да |
| A ∨ (B ∧ C) | (A ∨ B) ∧ C | Нет |
Приведенные примеры демонстрируют различные случаи определения эквивалентности двух формул. В некоторых случаях формулы оказываются эквивалентными, а в других - нет. Используя различные методы и приёмы, математики и логики могут определить, являются ли две формулы эквивалентными или нет, что позволяет упростить решение многих задач и доказательств.
Пример с использованием таблицы истинности
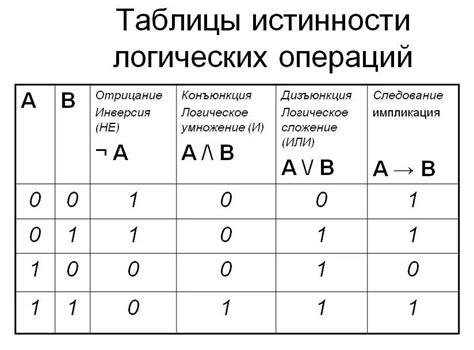
Для определения эквивалентности двух логических формул можно использовать таблицу истинности. Рассмотрим пример двух формул:
Формула А: (p ∨ q) → r
Формула В: ¬p → (¬q ∨ r)
Создадим таблицу истинности, где будут перечислены все возможные комбинации значений переменных p, q и r:
| p | q | r | (p ∨ q) → r | ¬p → (¬q ∨ r) | Эквивалентны? |
|---|---|---|---|---|---|
| И | И | И | И | И | Да |
| И | И | Л | Л | Л | Да |
| И | Л | И | И | И | Да |
| И | Л | Л | Л | Л | Да |
| Л | И | И | И | И | Да |
| Л | И | Л | Л | Л | Да |
| Л | Л | И | И | И | Да |
| Л | Л | Л | Л | Л | Да |
Из таблицы видно, что значения логических формул для всех комбинаций переменных p, q и r одинаковы. Таким образом, формула А и формула В эквивалентны друг другу.
Пример с использованием алгоритма эквивалентности
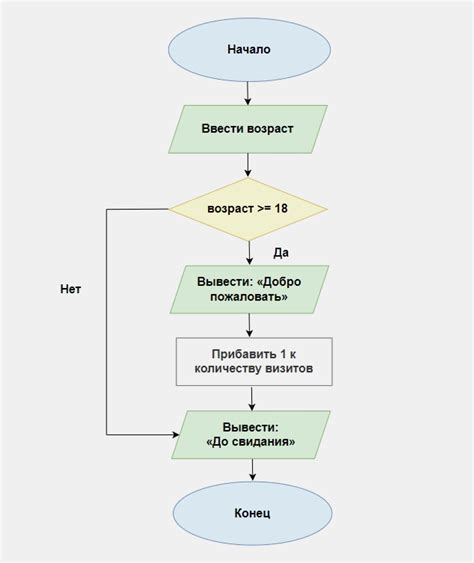
Представим, что у нас есть две логические формулы: A := (p ∧ q) ∨ r и B := (p ∨ ¬q) ∧ (p ∨ r).
Чтобы проверить эквивалентность этих формул, мы можем использовать алгоритм эквивалентности, который позволяет сравнивать формулы на основе их истинностных значений.
Сначала мы создадим таблицу истинности для формул A и B:
| p | q | r | (p ∧ q) ∨ r | (p ∨ ¬q) ∧ (p ∨ r) |
| true | true | true | true | true |
| true | true | false | true | true |
| true | false | true | true | true |
| true | false | false | false | false |
| false | true | true | true | true |
| false | true | false | false | false |
| false | false | true | true | true |
| false | false | false | false | false |
После этого мы сравниваем значения для каждой комбинации истинностных значений. Если значения совпадают для всех комбинаций, то формулы эквивалентны. В данном примере значения совпадают для всех комбинаций, поэтому мы можем заключить, что формулы A и B эквивалентны друг другу.
Алгоритм эквивалентности позволяет обнаруживать связь между логическими формулами и определять их эквивалентность. Это полезный инструмент при анализе и оптимизации логических выражений.



