Дроби - это числа, которые образованы двумя числами, разделенными чертой. Обычно мы знакомы с операциями сложения, вычитания, умножения и деления на целых числах. Но что делать, если в неравенстве встречаются дроби? Можно ли умножать на знаменатель? Ответ на этот вопрос - да, можно умножать на знаменатель в неравенстве, но при этом нужно быть осторожным, чтобы не нарушить правила манипулирования неравенствами.
При умножении или делении обеих частей неравенства на положительное число знак неравенства не меняется. Однако, если мы умножаем или делим на отрицательное число, например, когда имеем дело с отрицательной дробью, то знак неравенства меняется на противоположный. Поэтому важно всегда проверять знак числа или дроби, на которое мы умножаем или делим неравенство.
Рассмотрим пример для наглядности. Пусть имеется неравенство 3/4 < 2/5. Чтобы избавиться от знаменателей, мы можем умножить обе части неравенства на 20 (наименьшее общее кратное 4 и 5). Получим: 3/4 * 20 < 2/5 * 20. Упростив выражение, получим: 15 < 8. Ясно, что это неверное утверждение, поэтому и исходное неравенство неверно.
Можно ли умножать на знаменатель в неравенстве?

При решении неравенств важно помнить, что умножение или деление обеих сторон неравенства на положительное число не меняет его направление. Однако, если мы умножаем или делим на отрицательное число, то направление неравенства меняется.
Что же касается умножения на знаменатель в неравенстве, то здесь нужно быть осторожным. Для некоторых знаменателей, умножение на знаменатель может привести к изменению неравенства.
Позволю себе привести пример: если имеется неравенство a/b > c, где а и b - числа, и b больше нуля, то умножение обеих сторон на b сохранит направление неравенства. Ответом будет a > b*c. Но, если b меньше нуля, то направление неравенства изменится, и ответ будет a < b*c.
Таким образом, можно умножать на знаменатель в неравенстве, но важно помнить о знаке знаменателя и его влиянии на направление неравенства. Обратите внимание, что в случае с дробями умножение на знаменатель может привести к появлению дополнительных условий, связанных со знаком числителя.
Правила работы с дробями в неравенствах и возможность умножения на знаменатель
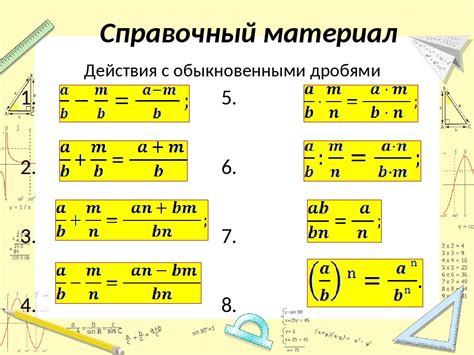
Одно из основных правило состоит в том, что если умножить или разделить обе части неравенства на положительное число, то неравенство сохранит свою ориентацию. То есть, если имеется неравенство a/b < c/d, где a, b, c и d являются числами, и b и d положительными числами, то умножение обеих частей неравенства на bd дает результат ad < bc.
При умножении на знаменатель дроби, необходимо учитывать его знак. Если знаменатель является положительным числом, то умножение на него не меняет направление неравенства. Например, если имеется неравенство a/b < c, где a и b являются числами, а b положительным числом, то умножение обеих частей неравенства на b дает результат a < bc.
Однако, если знаменатель является отрицательным числом, то при умножении на него необходимо изменить направление неравенства. Например, если имеется неравенство a/b < c, где a и b являются числами, а b отрицательным числом, то умножение обеих частей неравенства на b дает результат a > bc.
Важно помнить, что при умножении или делении на отрицательное число, необходимо изменить направление неравенства. Однако, стоит отметить, что эти правила применимы только при положительных знаменателях дробей.
Как действовать с дробями в неравенствах?

Работа с дробями в неравенствах имеет свои особенности, однако базовые правила остаются прежними. Важно помнить, что при умножении или делении на отрицательное число, направление неравенства меняется.
Рассмотрим простой пример: неравенство $\frac{x}{2} \lt 3$. Чтобы избавиться от знаменателя и упростить неравенство, нужно умножить обе части на 2:
$2 \cdot \frac{x}{2} \lt 2 \cdot 3$.
После упрощения получаем $x \lt 6$. Итак, ответом является интервал значений переменной $x$, при которых выполнено исходное неравенство.
Однако, существует одно важное ограничение: нельзя умножать или делить на 0. Если в дроби или знаменателе присутствует переменная, то нужно учитывать это ограничение в решении неравенства.
Например, рассмотрим неравенство $\frac{x-3}{x} \gt 0$. В данном случае, знаменатель не может быть равен 0, поэтому необходимо найти все значения переменной $x$, при которых выполняется неравенство, исключая значение, при котором знаменатель обращается в 0.
Основные шаги по работе с дробями в математических неравенствах

Решение математических неравенств, содержащих дроби, требует определенных действий, чтобы получить правильный ответ. Дроби представляются в виде частного двух чисел, и при работе с ними необходимо учитывать особенности их умножения и деления.
Основные шаги по работе с дробями в математических неравенствах:
- Переместите все дроби на одну сторону неравенства. В результате получим неравенство вида a/b < c/d, где a/b и c/d – дроби.
- Избавьтесь от знаменателей, умножив обе части неравенства на наименьшее общее кратное (НОК) знаменателей a/b и c/d. Это позволит нам избавиться от дробей и получить неравенство целых чисел.
- Продолжайте решать полученное неравенство как обычное математическое выражение. Выполняйте операции с числами, соблюдая правила математики.
- Если необходимо, упростите полученное выражение, чтобы найти значения переменных или найти конкретное решение неравенства.
Важно помнить, что при умножении или делении на отрицательное число знак неравенства меняется на противоположный. Также стоит обратить внимание на особенности работы с неравенствами, которые имеют отрицательную степень или отрицательные корни.
Применение этих шагов позволит вам эффективно работать с дробями в математических неравенствах и получать правильные решения. Она также позволит избегать ошибок и значительно упростит процесс решения неравенств с дробными значениями.
Разбор примеров использования дробей в неравенствах

Использование дробей в неравенствах может иногда представлять сложность, но при некоторой практике и понимании основных правил, они становятся более понятными. Давайте рассмотрим несколько примеров, чтобы лучше понять, как действовать с дробями в неравенствах.
Пример 1:
Решим неравенство 2/x < 5.
Для начала, перепишем неравенство без дроби:
2/x < 5 => 2 < 5x
Теперь давайте избавимся от дроби и решим новое неравенство:
2 < 5x => x > 2/5
Итак, решение это неравенство будет: x > 2/5.
Пример 2:
Решим неравенство 3/(2x - 4) > 1.
Для начала, перепишем неравенство без дроби:
3/(2x - 4) > 1 => 3 > 2x - 4
Теперь давайте избавимся от дроби и решим новое неравенство:
3 > 2x - 4 => 7 > 2x => x < 7/2
Итак, решение это неравенство будет: x < 7/2.
Пример 3:
Решим неравенство 1/x < 4 - 2/x.
Для начала, перепишем неравенство без дроби:
1/x < 4 - 2/x => 1/x - 2/x < 4 => -1/x < 4
Теперь давайте избавимся от дроби и решим новое неравенство:
-1/x < 4 => 1/x > -4
Обратите внимание, что при умножении неравенства на отрицательное число, символ неравенства меняет свое направление:
1/x > -4 => x < -1/4
Итак, решение это неравенство будет: x < -1/4.
Использование дробей в неравенствах может быть немного запутанным вначале, но при практике и понимании основных правил, вы можете легко справиться с такими задачами. Помните, что при умножении или делении на отрицательное число, направление неравенства изменяется, и всегда следите за условиями, чтобы избежать деления на ноль.
Практические примеры использования дробных чисел в неравенствах
Дробные числа находят широкое применение в математике, физике, экономике и других науках. В неравенствах они используются для сравнения и ограничения значений переменных.
Рассмотрим несколько практических примеров использования дробных чисел в неравенствах:
Пример 1:
Решим неравенство:
$$\frac{2}{3}x - \frac{5}{2} < 4$$
Для начала приведем дробные числа к общему знаменателю. В данном случае это $6$:
$$\frac{4}{6} = \frac{2}{3}$$
$$\frac{15}{6} = \frac{5}{2}$$
Теперь получаем:
$$\frac{2}{3}x - \frac{15}{6} < \frac{24}{6}$$
Упрощаем неравенство:
$$\frac{2}{3}x - \frac{5}{2} < 4$$
Умножим обе части неравенства на $6$ для избавления от знаменателя:
$$2x - 15 < 24$$
Теперь решим это неравенство относительно $x$:
$$2x < 24 + 15$$
$$2x < 39$$
$$x < \frac{39}{2}$$
Таким образом, решением данного неравенства является интервал $x \in (-\infty, \frac{39}{2})$.
Пример 2:
Решим неравенство:
$$-\frac{3}{4}x + \frac{5}{2} > \frac{7}{8}$$
Опять же приводим дробные числа к общему знаменателю, равному $8$:
$$-\frac{6}{8} = -\frac{3}{4}$$
$$\frac{10}{8} = \frac{5}{2}$$
$$\frac{7}{8} = \frac{7}{8}$$
Теперь получаем:
$$-\frac{3}{4}x + \frac{10}{8} > \frac{7}{8}$$
Упрощаем неравенство:
$$-\frac{3}{4}x + \frac{5}{2} > \frac{7}{8}$$
Умножим обе части неравенства на $8$:
$$-6x + 10 > 7$$
Теперь решим это неравенство относительно $x$:
$$-6x > 7 - 10$$
$$-6x > -3$$
$$x < \frac{-3}{-6}$$
$$x < \frac{1}{2}$$
Таким образом, решением данного неравенства является интервал $x \in (-\infty, \frac{1}{2})$.
Это лишь несколько примеров использования дробных чисел в неравенствах. В реальных задачах дроби могут быть более сложными, но принцип решения неравенств с дробными числами остается тем же: приведение дробей к общему знаменателю и последующие математические операции для нахождения диапазона значений переменных.



