Равнодействующая сил – это сила, которая равна сумме всех других сил, действующих на тело. В физике это понятие играет важную роль при анализе движения тел и определении их последствий.
Но что происходит, когда на тело действуют три силы, равные по модулю? Может ли равнодействующая этих трех сил быть нулевой? Чтобы ответить на этот вопрос, рассмотрим пример.
Представим себе три силы, действующие на тело в разных направлениях. Назовем эти силы силой A, силой B и силой C. Пусть каждая из этих сил имеет одинаковую величину, то есть A = B = C.
Если сумма всех трех сил равна нулю, то значит, что их равнодействующая также будет равна нулю. Однако, при условии, что все три силы равны по модулю, равнодействующая не может быть нулевой.
Может ли равнодействующая равных сил?

Равнодействующая трех равных по модулю сил не может быть равна нулю, если их направления не совпадают. Это означает, что приложение трех равных по модулю сил в разных направлениях будет создавать ненулевую равнодействующую силу.
Однако, если направления трех сил совпадают, то их равнодействующая будет равна нулю. Это означает, что трех равных сил, действующих в одном направлении, можно считать равнодействующей силой в покое.
Например, если есть три силы по 10 Н, направленные по горизонтали влево, их равнодействующая будет равна 0 Н, так как их векторные суммы будут компенсироваться.
Таким образом, равнодействующая трех равных по модулю сил может быть равной нулю только если они действуют в одном направлении, в противном случае она будет ненулевой.
Анализ примера

Для более наглядного объяснения ответа на вопрос о равнодействующей трех равных по модулю сил, рассмотрим следующий пример:
Предположим, у нас имеется три силы, действующие на тело, и все они имеют одинаковую величину и направление. В таком случае, мы можем сказать, что равнодействующая этих сил равна нулю.
Почему так происходит? Равнодействующая сил - это векторная сумма всех сил, действующих на тело. Если все силы равны по модулю и имеют одинаковое направление, то их векторы складываются друг с другом вдоль одной прямой. Таким образом, их сумма будет равна нулю, так как все векторы сил будут компенсировать друг друга.
Другими словами, если три силы одинаковы по модулю и направлены вдоль одной прямой, то они будут уравновешивать друг друга, и равнодействующая этих сил будет нулевой.
Однако, стоит отметить, что в реальных ситуациях силы могут иметь разные величины и направления, и тогда их равнодействующая будет отлична от нуля.
Определение равнодействующей силы
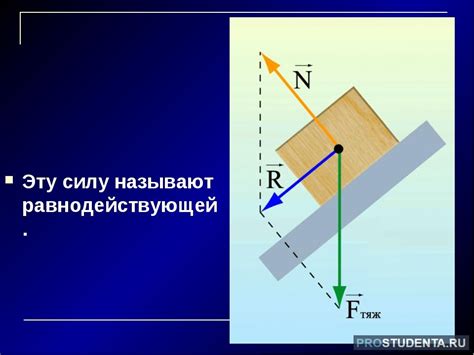
Для определения равнодействующей силы необходимо знать силы, действующие на тело, и их величины, а также учитывать направления сил. Если силы направлены в одном направлении, то векторная сумма сил будет равна алгебраической сумме их величин.
Например, если на тело действуют три силы, равные по модулю и направленные вдоль одной прямой, то равнодействующая сила будет равна сумме этих сил. В случае, когда силы направлены в разные стороны, необходимо учитывать их знаки при сложении векторов.
Определение равнодействующей силы является важным этапом анализа механической системы, так как позволяет определить, насколько общая сила воздействует на тело и в каком направлении она действует. Это позволяет предсказать движение и поведение тела под действием сил и применить соответствующие механические законы.
Принцип действия равнодействующей силы
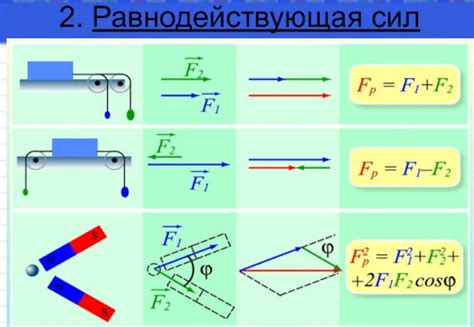
Принцип действия равнодействующей силы состоит в том, что если на объект действует несколько сил, то их векторная сумма, или равнодействующая сила, будет определять движение этого объекта. Если равнодействующая сила равна нулю, то объект остается в состоянии покоя или продолжает двигаться с постоянной скоростью.
Например, представим себе объект, на который действуют три равные по модулю силы, направленные в разные стороны. Если векторная сумма этих сил равна нулю, то объект будет оставаться в состоянии покоя или продолжит движение с постоянной скоростью. Если же равнодействующая сила не равна нулю, то объект будет изменять свое движение в направлении и со скоростью, определяемыми этой силой.
Принцип действия равнодействующей силы является основополагающим принципом в физике и используется для объяснения и предсказания движения всех объектов, от частиц и молекул до планет и звезд.
Иллюстрация на примере

Для более наглядного представления того, как работает равнодействующая трех равных по модулю сил, рассмотрим пример с двумя векторами.
Предположим, у нас есть две силы, направленные в разные стороны и равные по модулю. Пусть первая сила имеет векторное представление F₁ = 5 Н, а вторая сила - F₂ = 5 Н.
Если мы векторно сложим эти две силы, то получим их равнодействующую Fᵣ. По правилу параллелограмма или методу конечных проекций мы можем найти вектор Fᵣ, объединяющий начало первого вектора с концом второго.
В данном случае, равнодействующая Fᵣ будет равна 7.07 Н и будет направлена по диагонали параллелограмма, образованного силами F₁ и F₂. Таким образом, равнодействующая Fᵣ будет итоговой силой, действующей на объект.
Этот пример показывает, что равнодействующая трех равных по модулю сил также будет иметь свое векторное представление и будет равна геометрической сумме этих сил.
Равнодействующая трех равных по модулю сил: возможно ли?

Равнодействующая трех равных по модулю сил может быть как равна нулю, так и отлична от нуля, в зависимости от направления сил и их расположения. Определить возможность равнодействующей трех сил в конкретной ситуации можно с помощью графического или аналитического метода.
Рассмотрим пример: имеются три силы, равные по модулю и имеющие одно направление. В таком случае, равнодействующая этих сил также будет равна по модулю и направлена так же, как и каждая из сил. В этом случае равнодействующая сил будет равна сумме модулей исходных сил.
Однако, если силы имеют разные направления или разные точки приложения, то равнодействующая этих сил будет зависеть от угла между ними и их точек приложения. В таких случаях для определения равнодействующей трех сил необходимо использовать метод графической или аналитической суммы векторов.
| Случай | Равнодействующая |
|---|---|
| Силы равны по модулю и одно направление | Равна сумме модулей сил |
| Силы имеют разные направления или точки приложения | Зависит от угла между силами и их точками приложения |
Итак, равнодействующая трех равных по модулю сил зависит от условий их приложения. В некоторых случаях она может быть равна нулю, а в других - отличаться от нуля. Определение равнодействующей трех сил требует использования методов суммы векторов.



