Прямоугольник и ромб - две геометрические фигуры, которые отличаются своими основными свойствами. Возникает вопрос, может ли прямоугольник быть ромбом и под какими условиями это возможно.
Чтобы понять разницу между прямоугольником и ромбом, необходимо узнать их определение. Прямоугольник - это четырехугольник, у которого все углы прямые. Ромб - это четырехугольник, у которого все стороны равны друг другу.
Основное условие для прямоугольника - равенство двух попарно противоположных сторон. То есть, в прямоугольнике две стороны должны быть равны друг другу. Если все четыре стороны равны, то фигура является квадратом.
Основное условие для ромба - равенство всех четырех сторон. Если стороны прямоугольника равны между собой, то он может быть ромбом. Таким образом, ромб является частным случаем прямоугольника.
Определение прямоугольника и ромба
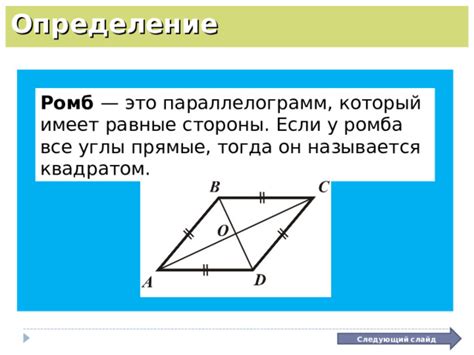
Ромб - это четырехугольник, у которого все стороны имеют одинаковую длину. Углы ромба не обязательно прямые, но при условии, что все углы ромба прямые, ромб превращается в квадрат.
Таким образом, прямоугольник является особым случаем ромба, когда углы ромба равны 90 градусам. Но ромб может иметь и другие углы, в отличие от прямоугольника.
Характеристики прямоугольника

1. Стороны: прямоугольник имеет две пары равных сторон, противоположные стороны имеют одинаковую длину. Обозначим эти стороны как a и b, где a - длина основания, b - длина высоты.
2. Периметр: периметр прямоугольника вычисляется по формуле P = 2(a + b), где P - периметр, a и b - длины сторон прямоугольника. Периметр прямоугольника равен сумме всех его сторон.
3. Площадь: площадь прямоугольника вычисляется по формуле S = a * b, где S - площадь, a и b - длины сторон прямоугольника. Площадь прямоугольника равна произведению длин его сторон.
4. Диагонали: прямоугольник имеет две диагонали - это отрезки, соединяющие противоположные вершины. Диагонали прямоугольника обладают несколькими свойствами, обозначим их как d1 и d2.
5. Углы: все углы прямоугольника равны 90 градусам. Обозначим эти углы как A, B, C и D. Углы A и C описывают основание прямоугольника, а углы B и D - его высоту.
Прямоугольник - это особый вид многоугольника с определенными характеристиками. Зная его основные свойства, можно легко определить, является ли данный четырехугольник прямоугольником или нет.
| Характеристика | Обозначение |
|---|---|
| Количество сторон | 4 |
| Количество углов | 4 |
| Параллельные стороны | 2 |
| Углы | 90 градусов |
Характеристики ромба

Характеристики ромба включают в себя:
1. Равные стороны: В ромбе все четыре стороны равны друг другу. Это означает, что длина каждой стороны ромба одинакова.
2. Равные углы: В ромбе все четыре угла равны между собой. Каждый угол ромба равен 90 градусов.
3. Диагонали: В ромбе имеется две диагонали, которые пересекаются в центре ромба. Диагонали ромба делят его на четыре равных треугольника.
4. Симметрия: Ромб обладает осью симметрии, проходящей через центр ромба и перпендикулярной каждой из его сторон. Каждая сторона и диагональ ромба являются осью симметрии.
Таким образом, ромб является особым типом прямоугольника, который отличается от остальных по своим характеристикам.
Равенство диагоналей в прямоугольнике

В прямоугольнике обе диагонали равны между собой. Это означает, что длина отрезка, соединяющего вершины, расположенные на противоположных сторонах, должна быть одинаковой.
Равенство диагоналей может быть проверено с помощью теоремы Пифагора. Если длины сторон прямоугольника удовлетворяют условию a^2 + b^2 = c^2, где a и b - длины сторон прямоугольника, а c - длина диагонали, то прямоугольник является также ромбом.
Завершая, следует отметить, что у прямоугольника необходимо выполнение других условий, таких как прямые углы и равенство смежных сторон, чтобы он мог быть ромбом. Равенство диагоналей является только одним из нескольких необходимых условий.
Неравенство сторон в ромбе

Чтобы прямоугольник стал ромбом, необходимо, чтобы все его четыре стороны имели одинаковую длину. Таким образом, если длины двух противоположных сторон прямоугольника не равны, он не может быть ромбом.
Равенство длин всех сторон является ключевым свойством, отличающим ромб от прямоугольника и других фигур. Необходимо помнить, что неравенство сторон в ромбе исключено.
| Прямоугольник | Ромб |
|---|---|
| Прямоугольник со сторонами разной длины | Ромб со сторонами одинаковой длины |
| AB ≠ BC | AB = BC = CD = DA |
Условия, при которых прямоугольник может быть ромбом
Чтобы прямоугольник мог быть ромбом, он должен удовлетворять определенным условиям. Вот основные из них:
- У прямоугольника все четыре стороны должны быть равными.
- Углы противоположных сторон прямоугольника должны быть равными. Все углы должны быть острыми.
- Соседние стороны прямоугольника должны быть перпендикулярными друг к другу.
Если прямоугольник удовлетворяет всем этим условиям, то его можно назвать ромбом. Из-за равенства сторон и углов, ромб имеет много симметрий и является особенным типом прямоугольника. Также стоит отметить, что все ромбы являются прямоугольниками, но не все прямоугольники являются ромбами.





