Образующая и высота - это два ключевых понятия, которые относятся к геометрии и широко используются при изучении конусов. Конус - это трехмерная геометрическая фигура, у которой основание представляет собой круг, а все точки боковой поверхности соединены с одной точкой - вершиной.
Высота конуса - это расстояние между вершиной и плоскостью основания. Образующая же - это линия, которая соединяет вершину конуса с точкой на его основании. Образующая может также рассматриваться как линия, определяющая форму и размеры боковой поверхности конуса.
Таким образом, ответ на вопрос о том, может ли образующая равняться высоте конуса, зависит от его формы. Если конус имеет правильную геометрическую форму, то да, образующая может быть равна высоте конуса. Это означает, что линия, соединяющая вершину и точку на основании, имеет ту же длину, что и расстояние от вершины до плоскости основания.
Математические свойства конуса

- Конус - геометрическое тело, которое образуется при вращении прямоугольного треугольника вокруг одного из его катетов.
- У конуса есть две основания - большая и малая окружности.
- Боковая поверхность конуса - это поверхность, которая соединяет вершину конуса с его основаниями и имеет форму равнобедренного треугольника.
- Образующая конуса - это отрезок, соединяющий вершину конуса с любой точкой на окружности его основания.
- Высота конуса - это отрезок, проведенный от вершины конуса до основания, перпендикулярно к плоскости основания.
- Если образующая конуса равна высоте, то такой конус называется правильным.
- В правильном конусе все боковые поверхности являются равнобедренными треугольниками.
- В правильном конусе угол между образующей и образующей на основании всегда равен углу между образующей и боковой стороной.
- Объем конуса можно вычислить по формуле: V = (1/3) * П * r^2 * h, где V - объем, П - пи, r - радиус основания, h - высота конуса.
- Площадь поверхности конуса можно вычислить по формуле: S = П * r * (r + l), где S - площадь, П - пи, r - радиус основания, l - образующая конуса.
Что такое конус
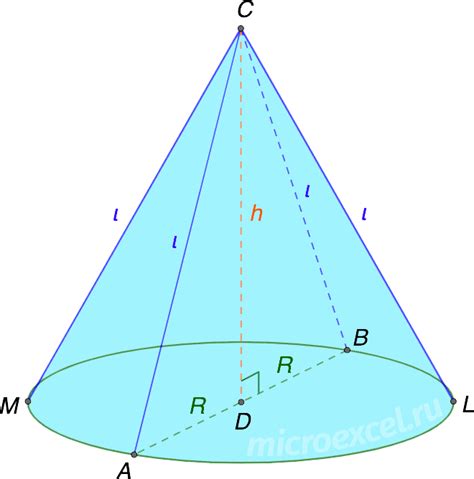
Основание конуса – это закрытая плоскость, которая лежит перпендикулярно к оси конуса и образована кривой линией, называемой контуром основания. Вершина конуса лежит на оси, которая проходит через центры оснований.
В высоте конуса лежит смысл его размерности. Она определяется как расстояние от вершины до плоскости основания, проходящей через центр основания. Образующая конуса – это линия, соединяющая вершину конуса с точками контура его основания. В случае, когда образующая равна высоте конуса, конус считается правильным.
Важно отметить, что радиусы оснований конуса обычно имеют разные значения, поэтому конус имеет форму усеченного конуса, а не прямого конуса.
Геометрические формулы конуса
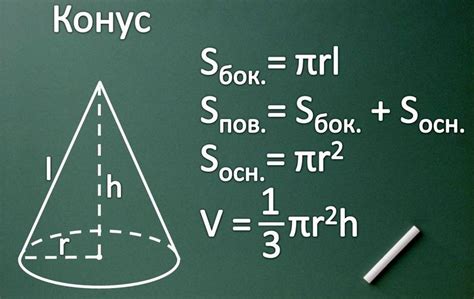
Одна из основных формул конуса - формула для вычисления площади поверхности. Площадь поверхности конуса можно найти, используя следующую формулу:
S = πr(r + l)
где S - площадь поверхности, r - радиус основания конуса, l - длина образующей конуса.
Также, для расчета объема конуса используется следующая формула:
V = (1/3)πr^2h
где V - объем конуса, r - радиус основания конуса, h - высота конуса.
И, наконец, для вычисления высоты конуса можно воспользоваться формулой:
h = √(l^2 - r^2)
где h - высота конуса, l - длина образующей конуса, r - радиус основания конуса.
Зная эти формулы, можно легко рассчитать характеристики и производить различные измерения конусов в геометрии.
Связь между радиусом основания и высотой
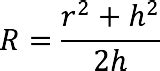
Во-первых, радиус основания определяет площадь основания конуса. Чем больше радиус, тем больше площадь основания. Это влияет на объем и плотность конуса.
Во-вторых, радиус основания также влияет на наклон боковой поверхности конуса. Чем больше радиус, тем более пологой становится боковая поверхность. При увеличении высоты, это может привести к увеличению наклона или уменьшению наклона пирамиды.
Наконец, радиус основания и высота конуса связаны через теорему Пифагора. Если мы знаем радиус и высоту, мы можем использовать эту теорему для вычисления длины образующей – гипотенузы треугольника, образованного радиусом, образующей и высотой.
Таким образом, радиус основания и высота конуса играют важную роль в его свойствах и можно сказать, что они взаимозависимы друг от друга.
Существуют ли конусы с равными образующими и высотами

Для начала, вспомним определение образующей конуса. Образующая – это прямая линия, соединяющая вершину конуса и точку на его основании. Высота конуса – это перпендикуляр, опущенный из вершины на плоскость основания.
Если образующая и высота конуса равны между собой, то такой конус называется равновысотным. Допустим, что образующая равна высоте конуса. Тогда мы можем представить такой конус в виде равнобедренного треугольника, у которого основаниями являются равносторонний треугольник, высотой конуса является его медиана.
Однако, стоит отметить, что равновысотные конусы являются относительно редким явлением. В большинстве случаев образующая и высота конуса будут отличаться друг от друга. Конусы с равными образующими и высотами могут быть особенными и интересными объектами, но в обычной практике такие конусы встречаются редко.
В таблице ниже приведены примеры конусов с разными значениями образующих и высот:
| Образующая | Высота |
|---|---|
| 5 см | 4 см |
| 10 см | 8 см |
| 15 см | 12 см |
Из таблицы видно, что значения образующих и высот различны, что указывает на то, что образующая и высота конуса обычно не равны друг другу.
Таким образом, можно заключить, что конусы с равными образующими и высотами существуют, но они являются исключительными случаями. Большинство конусов имеют различные значения образующих и высот, что делает равновысотные конусы интересными объектами и исследованиями в геометрии.
Примеры и контрпримеры

В данном разделе мы рассмотрим несколько примеров, которые помогут нам лучше понять, может ли образующая равняться высоте конуса.
Пример 1: Предположим, что у нас есть конус, у которого высота равна 10 см, а образующая равна 8 см. В данном случае образующая не может равняться высоте конуса, так как она меньше высоты.
Пример 2: Предположим, что у нас есть конус, у которого высота равна 6 см, а образующая равна 6 см. В данном случае образующая может равняться высоте конуса, так как они имеют одинаковое значение.
Пример 3: Предположим, что у нас есть конус, у которого высота равна 12 см, а образующая равна 14 см. В данном случае образующая не может равняться высоте конуса, так как она больше высоты.
Практическое применение математических свойств конуса

1. Инженерное строительство:
Математические свойства конуса широко применяются в инженерном строительстве. Один из примеров - использование конусов для создания стабильных и прочных строительных опор. Благодаря своей форме, конусы обладают высокой стойкостью к внешним нагрузкам, что делает их идеальным выбором для поддерживающих структур.
2. Объемные емкости:
Конусы также широко используются при проектировании различных объемных емкостей, таких как баки, цистерны, водонапорные башни и другие. Благодаря своим математическим свойствам, создание конических емкостей позволяет максимально эффективно использовать объем и обеспечивает равномерное распределение давления внутри емкости.
3. Дизайн:
Конусы также активно применяются в дизайне и архитектуре. Этот геометрический элемент позволяет создать гармоничные и эффектные формы, которые придают уникальность и красоту различным объектам и зданиям. Конусы могут быть использованы в создании современного мебельного дизайна, архитектурных сооружений, скульптур и других предметов искусства.
4. Физика и астрономия:
Конусы имеют также широкое применение в физике и астрономии. Прямой и обратный конусы используются для фокусировки лучей света и звука в различных оптических и акустических системах. Коническая форма также характерна для некоторых природных явлений, таких как геометеорологические образования, образующиеся в атмосфере.



