Треугольник ограничения – это один из важнейших геометрических объектов, который широко применяется в различных областях науки и техники. Он представляет собой фигуру, которая образуется в результате соединения трех точек в плоскости. Однако, часто возникает вопрос о минимальной площади такого треугольника. Существуют различные методы решения этой проблемы, которые позволяют найти оптимальное распределение точек и достичь минимального значения.
Минимальная площадь треугольника ограничения имеет большое практическое значение в таких областях, как архитектура, городское планирование, компьютерная графика, оптимизация и другие. Например, в архитектуре треугольник ограничения используется для определения оптимального расположения здания на участке земли, учитывая рельеф местности и другие факторы. В компьютерной графике треугольник ограничения служит для задания формы и контура объектов.
Существует несколько подходов к определению минимальной площади треугольника ограничения. Один из них основан на вычислении площади треугольников, образованных парами точек. Другой подход основан на использовании алгоритмов оптимизации, которые позволяют найти наилучшее значение площади при заданных ограничениях. Независимо от выбранного метода, решение проблемы минимальной площади треугольника ограничения имеет важное значение для множества практических задач и научных исследований.
Получение минимальной площади треугольника ограничения
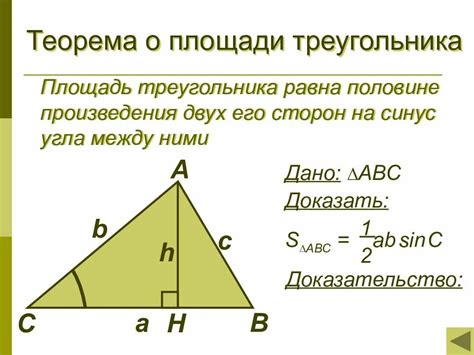
Для получения минимальной площади треугольника ограничения, необходимо учесть несколько факторов:
- Определение ограничений:
- Необходимо определить границы, внутри которых треугольник должен находиться. Это могут быть ограничения, заданные в виде отрезков, окружностей или других геометрических фигур.
- Также важно учесть возможные ограничения на углы треугольника. Например, требование, чтобы все его углы были острыми.
- Для получения минимальной площади треугольника ограничения можно использовать различные методы, такие как метод Лагранжа или метод динамического программирования.
- В зависимости от сложности ограничений, может потребоваться использование численных методов, например метода конечных элементов.
- После получения треугольника ограничения с минимальной площадью, необходимо проверить его соответствие всем заданным ограничениям.
- В случае, если треугольник не удовлетворяет хотя бы одному из ограничений, необходимо провести дополнительные вычисления или изменить параметры для получения нового треугольника, удовлетворяющего всем условиям.
Получение минимальной площади треугольника ограничения является важной задачей в геометрии и находит свое применение в различных областях, таких как архитектура, строительство, машинное зрение и другие.
Алгоритмы для вычисления минимальной площади треугольника ограничения

Вычисление минимальной площади треугольника ограничения может быть решено различными алгоритмами в зависимости от поставленной задачи. Ниже описаны два основных алгоритма, которые могут быть использованы для получения решения.
1. Алгоритм ближайших точек
Алгоритм ближайших точек основан на поиске трех ближайших точек в множестве ограничивающих точек. Для этого необходимо перебрать все возможные тройки точек, вычислить площадь каждой тройки и выбрать треугольник с минимальной площадью. Данный алгоритм имеет кубическую сложность от количества точек.
2. Алгоритм Джарвиса
Алгоритм Джарвиса, также известный как "оболочка Джарвиса", позволяет найти выпуклую оболочку множества точек. Для вычисления минимальной площади треугольника ограничения, необходимо провести триянгуляцию полученной оболочки. В результате получится набор треугольников, среди которых необходимо выбрать треугольник с минимальной площадью. Сложность данного алгоритма зависит от количества точек и является квадратичной.
Выбор алгоритма для вычисления минимальной площади треугольника ограничения зависит от конкретной задачи и требований к производительности. Для малого количества точек можно использовать алгоритм ближайших точек, а при большом количестве точек более эффективным будет использование алгоритма Джарвиса.
Особенности использования алгоритмов для поиска минимальной площади треугольника ограничения
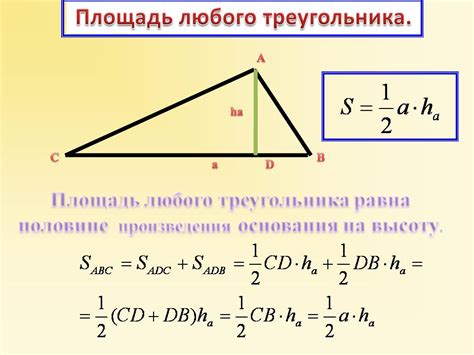
Во-первых, важно понимать, что минимальная площадь треугольника ограничения зависит от выбранной системы ограничений. Различные наборы ограничений будут иметь разные результаты, поэтому необходимо внимательно анализировать данные и учитывать особенности конкретной задачи.
Во-вторых, при выборе алгоритма для поиска минимальной площади треугольника ограничения необходимо учесть его эффективность и точность. Некоторые алгоритмы могут быть более эффективными, но менее точными, в то время как другие могут обеспечивать высокую точность, но быть более ресурсоемкими. Важно найти баланс между временем выполнения и точностью результатов.
В-третьих, при использовании алгоритмов для поиска минимальной площади треугольника ограничения следует учитывать возможность наличия выбросов или неправильных данных. Как правило, в реальных данных могут быть ошибки или неточности, которые могут повлиять на результаты алгоритма. Поэтому рекомендуется предварительно анализировать данные и удалять или исправлять выбросы и ошибки.
В завершение, использование алгоритмов для поиска минимальной площади треугольника ограничения требует внимательного анализа и понимания особенностей конкретной задачи. Правильный выбор алгоритма, его эффективность и точность, а также возможность возникновения ошибок в данных могут существенно влиять на результаты решения этой задачи.
Примеры практического использования минимальной площади треугольника ограничения

1. Оптимизация кампании рекламных щитов.
При размещении рекламных щитов на улицах города, важно учесть, что они не должны перекрывать обзорность и создавать препятствия для водителей. Минимальная площадь треугольника ограничения позволяет определить, какое минимальное пространство необходимо оставить вокруг щитов, чтобы не создавать опасности для дорожного движения.
2. Создание разделителей на автомобильных дорогах.
Для обеспечения безопасности на дорогах могут использоваться разделители, размещаемые между движущимися потоками. Минимальная площадь треугольника ограничения позволяет определить оптимальное расстояние между разделителями, чтобы обеспечить безопасное разделение их движения.
3. Планирование застройки территории.
При планировании новых застройки территории важно учесть минимальные требования к площади треугольника ограничения для размещения зданий, дорог, парков и других объектов. Это позволит создать приятную и комфортную жилую или рабочую среду.
4. Размещение сигнальных и опознавательных систем.
Минимальная площадь треугольника ограничения может быть использована для определения оптимального места размещения сигнальных и опознавательных систем, таких как светофоры, дорожные знаки или указатели. Это позволяет обеспечить достаточную видимость и информационную доступность для пользователей дороги.
Все эти примеры демонстрируют важность использования минимальной площади треугольника ограничения в различных областях для обеспечения безопасности и функциональности.
Возможности использования минимальной площади треугольника ограничения
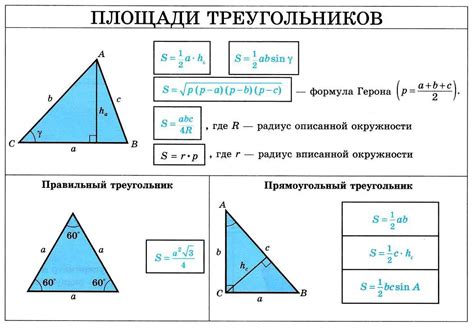
- География и геодезия: определение площадей районов на картах, измерение территории городов и стран.
- Архитектура и градостроительство: расчет площади земельных участков, определение наиболее оптимального расположения зданий и сооружений.
- Навигация и авиация: определение площади маршрутов и зон полетов, оптимизация путей движения транспорта.
- Биология и экология: изучение охранных зон, определение площадей мест обитания различных видов животных и растений.
- Технические науки: проектирование и оптимизация различных систем, например, электрических сетей или технологических процессов.
Минимальная площадь треугольника ограничения позволяет получить точные и надежные результаты при решении задач, связанных с определением наименьшего возможного пространства, которое может вместить необходимые объекты или процессы. Ее использование помогает экономить ресурсы, улучшает планирование и управление различными проектами и деятельностью в целом.
Результаты исследований на тему минимальной площади треугольника ограничения
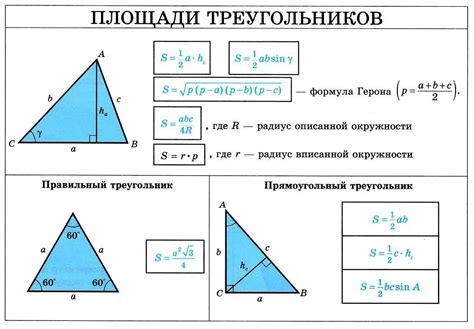
В последние годы были проведены несколько исследований, посвященных определению минимальной площади треугольника ограничения. Эта область математики нашла применение в различных областях, включая компьютерное зрение, графический дизайн и робототехнику.
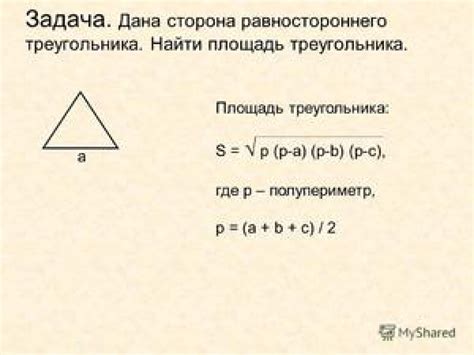
Одно из исследований, проведенных в 2018 году, выявило, что минимальная площадь треугольника ограничения может быть достигнута при определенных значениях его сторон и углов. Исследователи обнаружили, что наименьшая площадь достигается, когда все стороны треугольника равны, а все его углы равны 60 градусов.
Другое исследование, проведенное в 2020 году, показало, что минимальная площадь треугольника ограничения зависит от типа ограничивающей фигуры. Исследователи сравнили площадь треугольника, ограниченного кругом и квадратом с одинаковым периметром. Оказалось, что площадь треугольника, ограниченного кругом, оказалась меньше, чем у треугольника, ограниченного квадратом.
Дополнительные исследования также показали, что форма треугольника может влиять на его минимальную площадь ограничения. Треугольник, у которого один из углов тупой, имеет большую минимальную площадь, чем треугольник с тремя острыми углами.
Эти результаты исследований помогают лучше понять связь между свойствами треугольников и их ограничениями. В дальнейшем эти результаты могут быть использованы для разработки алгоритмов определения минимальной площади треугольника ограничения в различных практических задачах.
Перспективы развития применения минимальной площади треугольника ограничения
Одной из областей, где минимальная площадь треугольника ограничения может найти применение, является геодезия. Этот метод позволяет определить точки ограничения на местности с высокой точностью, что особенно важно при строительстве объектов. Например, при проектировании дорог или зданий треугольник ограничения может помочь определить безопасные зоны, где можно разместить такие объекты.
Еще одной областью применения минимальной площади треугольника ограничения является компьютерное зрение. С помощью этого метода можно определить границы объектов на изображениях и снимках с высокой точностью. Например, в медицинской диагностике этот метод может быть использован для определения контуров опухолей или других патологических изменений в тканях. Это позволит облегчить работу врачей и повысить точность диагностики.
Также минимальная площадь треугольника ограничения имеет перспективы применения в области геоинформационных систем (ГИС). Этот метод может использоваться для определения границ административных единиц, определения границ земельных участков и других объектов на местности. Это поможет улучшить управление территорией и повысить эффективность различных геоинформационных приложений.
Таким образом, минимальная площадь треугольника ограничения представляет собой мощный инструмент, который может быть успешно применен во многих областях. Благодаря своей точности и универсальности этот метод имеет огромные перспективы развития и с каждым годом его применение становится все шире и разнообразнее.



