Линейная зависимость - это понятие, которое часто возникает при решении задач аналитической геометрии, математического анализа и алгебры. Понимание того, являются ли заданные функции линейно зависимыми, является важным шагом в этих областях математики. Но как определить, являются ли функции линейно зависимыми?
Представим, что у нас есть набор функций, которые зависят от переменной x. Если существуют такие коэффициенты a1, a2, ..., an, не равные нулю, такие что уравнение a1 * f1(x) + a2 * f2(x) + ... + an * fn(x) = 0 выполняется для всех значений x, то функции являются линейно зависимыми.
С другой стороны, если такие коэффициенты существовать не могут, кроме случая, когда все a1, a2, ..., an равны нулю, то функции являются линейно независимыми. Это означает, что ни одна из функций не может быть выражена в виде линейной комбинации других функций.
Проверить, являются ли заданные функции линейно зависимыми, можно путем решения линейного уравнения a1 * f1(x) + a2 * f2(x) + ... + an * fn(x) = 0. Если существуют ненулевые значения коэффициентов a1, a2, ..., an, удовлетворяющие этому уравнению для всех значений x, то функции линейно зависимы.
Понятие линейной зависимости функций

Например, если есть две функции f(x) и g(x), то они будут линейно зависимыми, если существуют такие числа a и b, что a*f(x) + b*g(x) = 0 для всех значений x. Если нет таких чисел a и b, то функции считаются линейно независимыми.
Основные признаки линейно зависимых функций:
- Существует нетривиальная линейная комбинация функций, дающая ноль.
- Одна функция может быть выражена через другую функцию или несколько функций.
- Линейно зависимые функции лежат в одной плоскости или пространстве.
Важно отметить, что линейная зависимость функций может быть проверена путем решения системы линейных уравнений или анализа их графиков. Понимание линейной зависимости функций позволяет решать множество задач в различных областях математики и физики.
Критерии для определения линейной зависимости
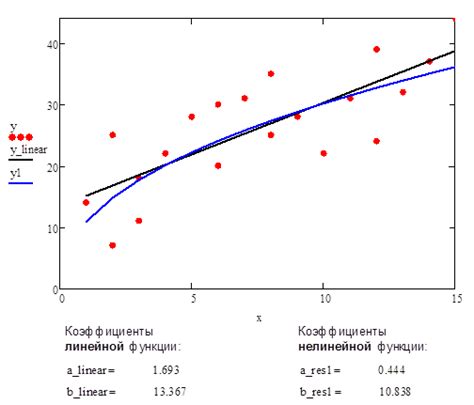
Линейная зависимость возникает, когда некоторые функции могут быть выражены в виде линейных комбинаций других функций. Для определения линейной зависимости можно использовать несколько критериев:
- Сумма коэффициентов равна нулю. Если для функций f1, f2, ..., fn существуют такие числа с1, с2, ..., сn, что c1f1 + c2f2 + ... + cnfn = 0, и при этом не все коэффициенты ci равны нулю, то функции линейно зависимы.
- Определитель равен нулю. Матрица, составленная из коэффициентов перед функциями, называемых также линейными комбинациями, является вырожденной, то есть ее определитель равен нулю.
- Одна функция является линейной комбинацией других функций. Если одну из данных функций можно выразить в виде линейной комбинации других функций, то они считаются линейно зависимыми.
- Один из векторов является линейной комбинацией других векторов. Если один из векторов набора можно выразить в виде линейной комбинации других векторов этого набора, то они линейно зависимы.
При выполнении хотя бы одного из этих критериев функции можно считать линейно зависимыми. Используя эти критерии, можно определить линейность функций и использовать эту информацию для решения различных задач в математике и физике.
Линейная зависимость векторов

Для проверки линейной зависимости векторов можно использовать следующий алгоритм:
- Записать векторы в виде столбцов матрицы. Каждый вектор будет представлен как столбец с соответствующими элементами.
- Решить систему уравнений, получившуюся при равенстве линейной комбинации векторов нулевому вектору. Для этого нужно приравнять столбцы матрицы с векторами к нулевому столбцу.
- Если получилось ненулевое решение системы, то векторы являются линейно зависимыми. Если же получилась тривиальная система с нулевым решением, то векторы линейно независимы.
Пример проверки линейной зависимости векторов можно представить следующим образом:
| 1 4 6 | | 0 | | -2 -5 1 | -----> | 0 | | 3 2 0 | | 0 |
Это эквивалентно следующей системе уравнений:
x + 4y + 6z = 0 -2x - 5y + z = 0 3x + 2y = 0
Решив эту систему, мы получим, что x, y и z равны нулю. Следовательно, вектора являются линейно независимыми.
Изучение линейной зависимости векторов является важным шагом в решении различных задач линейной алгебры и имеет множество практических применений в физике, программировании, экономике и других областях.
Обратная линейная зависимость функций
Для определения обратной линейной зависимости необходимо проанализировать коэффициент корреляции между двумя функциями, который может принимать значения от -1 до 1.
Если коэффициент корреляции равен -1, это означает, что изменение одной функции полностью обусловливает противоположное изменение другой функции. Например, при увеличении одной функции на единицу, другая функция будет уменьшаться на такую же величину.
Определение обратной линейной зависимости может быть полезно в различных областях, таких как физика, экономика, социология. Например, в экономике обратная линейная зависимость может проявляться между ценой и спросом на товар: при увеличении цены на товар спрос на него снижается.
| Коэффициент корреляции | Вид линейной зависимости |
|---|---|
| -1 | Обратная линейная зависимость |
| 0 | Отсутствие линейной зависимости |
| 1 | Прямая линейная зависимость |
Проверка линейной зависимости функций

Один из таких методов - метод определителей. Сначала составляются уравнения вида:
a1f1(x) + a2f2(x) + ... + anfn(x) = 0
где a1, a2, ..., an - произвольные числа, f1(x), f2(x), ..., fn(x) - проверяемые функции.
Затем составляется определитель:
| a1 a2 ... an |
| f1(x) f2(x) ... fn(x) |
Если определитель равен нулю для всех значений x, то функции линейно зависимы, иначе они линейно независимы.
Другой метод - метод коэффициентов. Для этого составляется система уравнений:
a1f1(x) + a2f2(x) + ... + anfn(x) = 0
a1f1'(x) + a2f2'(x) + ... + anfn'(x) = 0
...
a1f1(n-1)(x) + a2f2(n-1)(x) + ... + anfn(n-1)(x) = 0
где f1'(x), f2'(x), ..., fn'(x) - производные функций f1(x), f2(x), ..., fn(x) соответственно.
Эта система имеет ненулевое решение a1, a2, ..., an только тогда, когда функции линейно зависимы.
Также можно использовать графический метод. Для этого строится график каждой функции на одном координатном поле. Если все графики лежат на одной прямой или на одной поверхности, то функции линейно зависимы. В противном случае они линейно независимы.
Важно помнить, что эти методы являются приближенными и могут давать неверные результаты из-за ошибок округления или других факторов.
Доказательство независимости функций
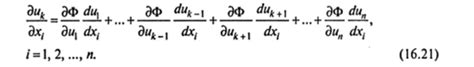
Существуют несколько способов доказательства независимости функций:
1. Метод коэффициентов
В этом методе мы предполагаем, что функции являются линейно зависимыми и пытаемся найти коэффициенты, при которых их линейная комбинация равна нулевой функции. Если получается найти такие коэффициенты, то функции являются линейно зависимыми. В противном случае они являются независимыми.
2. Метод определителей
В этом методе мы строим матрицу из коэффициентов при функциях и вычисляем ее определитель. Если определитель равен нулю, то функции являются линейно зависимыми. Если определитель не равен нулю, то функции являются независимыми.
3. Метод размерностей
В этом методе мы сравниваем количество функций с размерностью пространства, в котором они определены. Если количество функций больше размерности пространства, то они являются линейно зависимыми. Если количество функций равно размерности пространства, то они являются независимыми.
Доказательство независимости функций является основой для решения множества математических и физических задач. Правильное применение методов доказательства независимости функций помогает обнаружить и изучить линейные зависимости между функциями и применить их для получения новых результатов.



