Как узнать является ли число корнем квадратного уравнения?
Квадратное уравнение – это одно из основных понятий в математике, которое возникает при решении различных задач. Чтобы найти корни квадратного уравнения, нужно знать его коэффициенты a, b и c. Однако, что делать, если нам дано число, и мы хотим узнать, является ли оно корнем данного уравнения?
Существует простой способ проверить, является ли число корнем квадратного уравнения. Нужно подставить это число вместо переменной x в уравнение и произвести несложные арифметические вычисления. Если после вычислений получится верное равенство, то это число является корнем уравнения, в противном случае оно не является корнем.
Чтобы это более наглядно объяснить, рассмотрим пример. Пусть дано квадратное уравнение x^2 + 2x - 3 = 0. Чтобы узнать, является ли число 1 корнем этого уравнения, нужно подставить его вместо переменной x: (1)^2 + 2(1) - 3 = 1 + 2 - 3 = 0. Таким образом, число 1 является корнем данного уравнения.
Понятие квадратного уравнения

ax^2 + bx + c = 0
где a, b и c – это коэффициенты уравнения, причем a ≠ 0.
Корни квадратного уравнения представляют собой значения переменной x, при которых уравнение принимает значение 0. То есть, если x является корнем уравнения, то значение выражения ax^2 + bx + c равно 0.
Квадратные уравнения имеют три возможных случая:
- Если дискриминант D = b^2 - 4ac равен нулю, то уравнение имеет один действительный корень. Этот корень будет графически представлять собой точку, где парабола, описываемая уравнением, касается оси x.
- Если дискриминант D > 0, то уравнение имеет два различных действительных корня. Графически это представляет собой точки пересечения параболы с осью x.
- Если дискриминант D < 0, то уравнение не имеет действительных корней. В этом случае корни являются комплексными числами.
Решение квадратных уравнений может быть выполнено с помощью различных методов, таких как по формуле дискриминанта или методом завершения квадрата. Знание понятия квадратного уравнения и его свойств позволяет определить, является ли данное число корнем этого уравнения и решить уравнение в целом.
Методы решения квадратных уравнений

Существуют несколько методов решения квадратных уравнений:
- Метод дискриминанта. Этот метод основан на вычислении дискриминанта D = b^2 - 4ac. Если D > 0, то уравнение имеет два различных корня; если D = 0, то уравнение имеет один корень; если D < 0, то уравнение не имеет действительных корней.
- Метод рационализации. С помощью этого метода можно решить уравнения вида (a + √b)^2 = c или (a - √b)^2 = c, где a, b и c - заданные числа. Рационализация позволяет избавиться от корня и решить уравнение.
- Метод факторизации. Если квадратное уравнение может быть факторизовано, то его можно решить путем разложения на множители и нахождения значений, при которых каждый из множителей равен нулю.
- Метод завершения квадратного трехчлена. Этот метод основан на преобразовании уравнения ax^2 + bx + c = 0 в вид (x + p)^2 = q, где p и q - заданные числа. Затем находятся значения переменной x, удовлетворяющие данному равенству.
Выбор метода решения квадратного уравнения зависит от формы самого уравнения и требуемой точности.
Знание методов решения квадратных уравнений позволяет находить корни уравнений и использовать их в различных областях, таких как физика, математика, экономика и т.д.
Корень квадратного уравнения
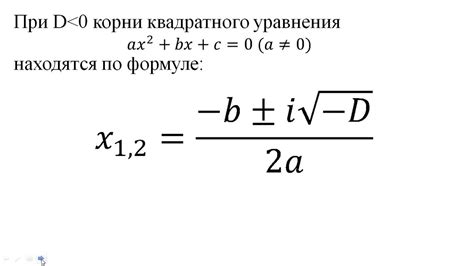
Квадратное уравнение имеет вид: ax2 + bx + c = 0, где a, b и c - коэффициенты уравнения, причем a ≠ 0.
Для определения корней квадратного уравнения можно использовать дискриминант. Дискриминант вычисляется по формуле: D = b2 - 4ac.
Если дискриминант больше нуля, то уравнение имеет два различных вещественных корня. Если дискриминант равен нулю, то уравнение имеет один вещественный корень (корень кратности 2). Если дискриминант меньше нуля, то уравнение не имеет вещественных корней, но имеет два комплексных корня.
Таблица ниже показывает связь между значением дискриминанта и количеством корней квадратного уравнения:
| Значение дискриминанта (D) | Количество корней |
|---|---|
| D > 0 | 2 различных вещественных корня |
| D = 0 | 1 вещественный корень (корень кратности 2) |
| D < 0 | нет вещественных корней, 2 комплексных корня |
Подставляя значение переменной в уравнение, можно проверить, является ли число корнем квадратного уравнения. Если результат уравнения равен нулю, то число является корнем уравнения. В противном случае, число не является корнем уравнения.
Как проверить число на корень квадратного уравнения

- Возьмите данное число и раскройте скобки в квадратном уравнении, заменяя переменную на это число.
- Вычислите полученное выражение, используя законы арифметики.
- Если результат вычислений равен нулю, то данное число является корнем квадратного уравнения.
Если результат не равен нулю, то данное число не является корнем квадратного уравнения.
Например, если дано уравнение x^2 - 4x + 4 = 0, и нам нужно проверить, является ли число 2 корнем этого уравнения, мы можем выполнить следующие шаги:
- Возьмите число 2 и подставьте его вместо x в уравнение: (2)^2 - 4(2) + 4 = 0.
- Вычислите результат: 4 - 8 + 4 = 0.
- Поскольку результат равен нулю, число 2 является корнем квадратного уравнения.
Таким образом, мы можем проверить любое число на корень квадратного уравнения, следуя приведенным выше шагам.
Примеры

Пример 1: Известно квадратное уравнение x^2 - 5x + 6 = 0. Чтобы узнать, является ли число 2 корнем этого уравнения, нужно подставить 2 вместо x и проверить, что получится равенство (2)^2 - 5(2) + 6 = 4 - 10 + 6 = 0. Если полученное значение равно 0, то число 2 является корнем уравнения.
Пример 2: Рассмотрим квадратное уравнение y^2 - 3y + 2 = 0. Для проверки, является ли число 1 корнем этого уравнения, подставим 1 вместо y и проверим, что получится равенство (1)^2 - 3(1) + 2 = 1 - 3 + 2 = 0. Если полученное значение равно 0, то число 1 является корнем уравнения.
Пример 3: Предположим, у нас есть квадратное уравнение z^2 - 6z + 8 = 0. Чтобы выяснить, является ли число 3 корнем этого уравнения, подставим 3 вместо z и проверим, что получится равенство (3)^2 - 6(3) + 8 = 9 - 18 + 8 = -1. Если полученное значение не равно 0, то число 3 не является корнем уравнения.
Таким образом, путем подстановки числа вместо неизвестной переменной и проверки равенства нулю, мы можем определить, является ли число корнем квадратного уравнения.
- Для проверки, является ли число корнем квадратного уравнения, необходимо вставить данное число в уравнение и проверить, выполняется ли равенство.
- Если при подстановке числа в уравнение обе его стороны равны, то число является корнем квадратного уравнения.
- Если при подстановке числа в уравнение обе его стороны не равны, то число не является корнем квадратного уравнения.
- Для поиска корней квадратного уравнения можно использовать формулу дискриминанта.
- Принимая во внимание дискриминант, можно определить, сколько корней имеет квадратное уравнение: два различных, один или ни одного.



