Математика – это не только абстрактные формулы и сложные уравнения, но и ежедневные задачи, с которыми мы сталкиваемся повсюду. Одной из таких задач является определение, поместится ли круг в квадрате. Это имеет практическое значение при размещении объектов на плоскости, проектировании и многих других областях. Давайте разберемся, как можно решить эту интересную задачу!
Чтобы понять, поместится ли круг в квадрате, нужно знать их геометрические свойства. Круг – это фигура, образуемая всеми точками, находящимися на одинаковом расстоянии от центра, а в квадрате все стороны равны друг другу. Для того чтобы найти решение задачи, мы должны учесть различные варианты положения круга внутри квадрата.
Первый случай – круг полностью помещается внутри квадрата. Это возможно, когда диаметр круга не превышает длину стороны квадрата. В этом случае, если радиус окружности равен половине стороны квадрата, круг точно поместится внутри него. Но что, если диаметр круга больше стороны квадрата? Давайте рассмотрим другие варианты!
Как проверить, что круг поместится в квадрате?

Если у вас есть круг и квадрат, вы можете проверить, поместится ли круг внутри квадрата, следуя этим шагам:
- Убедитесь, что у вас есть измерения круга и квадрата. Вам понадобится радиус круга и длина стороны квадрата.
- Вычислите диаметр круга, умножив радиус на 2.
- Сравните диаметр круга с длиной стороны квадрата. Если диаметр круга меньше или равен длине стороны квадрата, то круг поместится внутри квадрата.
- Проверьте, что центр круга находится внутри квадрата. Если центр круга находится в пределах сторон квадрата, то круг поместится полностью внутри квадрата.
Теперь вы знаете, как проверить, поместится ли круг в квадрате. Этот метод полезен при решении различных геометрических задач или при планировании использования пространства.
Метод нахождения площади фигур
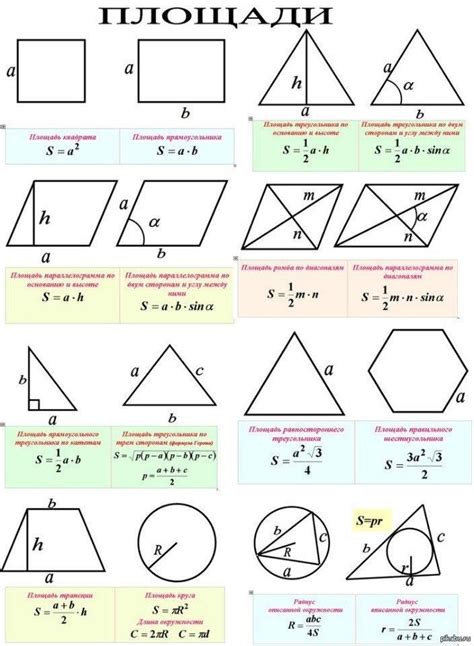
Существует несколько методов нахождения площади различных геометрических фигур:
- Для прямоугольника: площадь равна произведению длины одной стороны на длину другой стороны.
- Для треугольника: площадь можно найти с помощью формулы Герона или как половину произведения длины основания на высоту.
- Для круга: площадь можно вычислить по формуле πr2, где π – это математическая константа, а r – радиус круга.
- Для квадрата: площадь равна квадрату длины одной из его сторон.
Зная эти формулы, можно легко находить площади различных фигур. Они широко применяются в геометрии, а также в различных областях, связанных с измерениями и вычислениями площадей.



