Квадрат - это одна из самых основных геометрических фигур. У него четыре стороны, все углы равны и размеры сторон также равны. Но, помимо этого, квадрат обладает еще одной интересной особенностью – его диагонали делят все углы пополам.
Однако, если мы взглянем на треугольники AOB и BOC, то заметим, что они оба имеют две равные стороны и общую вершину O. Следовательно, эти треугольники равнобедренные. А значит, диагонали квадрата делят углы AOB и BOC пополам.
Таким образом, диагонали квадрата являются осью симметрии для всех его углов. Это свойство часто используется в решении геометрических задач и конструкции различных фигур. Поэтому, изучение и понимание этой особенности квадрата является важной частью геометрии.
Диагонали квадрата важны при делении углов
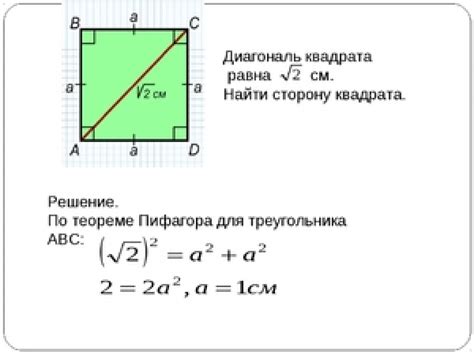
Одной из основных характеристик диагоналей квадрата является их способность делить углы пополам. Когда мы проводим диагональ внутри квадрата, она создает два равных угла внутри квадрата. Это свойство имеет важные геометрические и практические применения.
В геометрии, знание о том, что диагонали квадрата делят углы пополам, позволяет нам решить различные задачи, связанные с квадратами и их свойствами. Например, это позволяет нам находить углы квадрата, используя известные свойства и равенства. Также это помогает нам строить и изучать различные квадратные фигуры, основанные на диагоналях квадрата.
В практическом плане, знание о способности диагоналей квадрата делить углы пополам может быть полезным при проектировании и строительстве. Например, архитекторы и инженеры могут использовать это свойство для снижения веса и увеличения прочности конструкций. Также этот факт может быть использован для создания эффективных дизайнов и улучшения визуальной привлекательности различных объектов.
Таким образом, понимание и использование свойства диагоналей квадрата, которые делят углы пополам, является важным при изучении геометрии и ее практическом применении. Это свойство открывает перед нами новые возможности расширения знаний, улучшения навыков и творческого мышления.
Понятие квадрата и его особенности
| Стороны: | Все стороны квадрата одинаковой длины. |
| Углы: | Все углы квадрата равны 90 градусов. |
| Диагонали: | Диагонали квадрата равны друг другу и делят углы пополам. |
Благодаря равным сторонам и углам, квадрат является фигурой с простыми и легко расчитываемыми свойствами. Например, площадь квадрата можно вычислить, умножив длину стороны квадрата на самого себя (S = a * a), а периметр можно найти, умножив длину стороны на 4 (P = 4 * a).
Важной особенностью квадрата является то, что его диагонали равны друг другу и делят углы пополам. Диагонали квадрата также являются его осью симметрии, поэтому если провести две диагонали квадрата, он будет разделен на 4 равные части.
Диагонали квадрата и их свойства

Главная диагональ квадрата делит фигуру на два равных прямоугольных треугольника, при этом каждый из углов квадрата делится диагональю на два равных угла. Это свойство говорит о том, что главная диагональ квадрата делит углы пополам.
Побочная диагональ квадрата также делит фигуру на два равных прямоугольных треугольника, и каждый угол квадрата делится ею пополам.
Свойства диагоналей квадрата могут быть использованы для решения задач на нахождение углов, сторон и площади данной фигуры.
| Свойство диагоналей квадрата: |
|---|
| Главная диагональ делит углы квадрата пополам |
| Побочная диагональ делит углы квадрата пополам |
Используя данные свойства, можно легко решать задачи на нахождение неизвестных сторон и углов квадрата, а также на площадь этой фигуры.
Значимость деления углов при построении и анализе фигур
Диагонали квадрата, как известно, делят углы на две равные части. Это свойство квадрата позволяет использовать его для построения и измерения углов. Квадрат может служить эталоном для определения равенства других углов. Если углы двух фигур совпадают с углами квадрата, то они равны между собой.
Деление углов также широко применяется при анализе фигур. При нахождении площади фигуры, знание углов позволяет разбить фигуру на более простые геометрические элементы и использовать формулы для нахождения их площадей. Точное деление углов позволяет получить более точные результаты при анализе и измерении фигур.
Кроме того, деление углов влияет на внешний вид и эстетическое восприятие фигур. Равные углы и правильное деление углов способствуют симметричности и гармоничности фигур. Для дизайна и архитектуры также важно учитывать деление углов для создания привлекательных и эстетичных образов.



