Подготовка к ОГЭ по математике требует освоения не только различных теоретических понятий, но и знания некоторых важных формул. Они помогут не только справиться с заданиями на экзамене, но и решить множество жизненных задач. Поэтому нельзя недооценивать значимость формул в математике.
Одной из таких важных формул является формула площади прямоугольника. Для вычисления площади прямоугольника необходимо умножить длину одной из его сторон на длину другой стороны. Эта формула может быть очень полезной при решении задач, связанных с площадями и периметрами, а также при решении задач на вычисление площади поверхности тела.
Ещё одной из важных формул на ОГЭ является формула длины окружности. Длина окружности вычисляется как произведение числа пи на удвоенный радиус. Такая формула помогает вычислить длину окружности, а также решать задачи на вычисление длины дуги окружности.
Не менее важным является формула площади треугольника. Для вычисления площади треугольника необходимо умножить половину произведения длин его основания и высоты. Зная эту формулу, можно легко решить задачи на вычисление площадей треугольников, а также использовать её для решения задач на нахождение высоты треугольника или его основания.
Доступные формулы на ОГЭ по математике
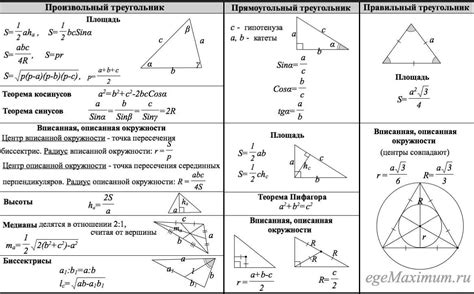
Вот некоторые из наиболее важных формул, которые стоит запомнить:
1. Формула для нахождения площади прямоугольника:
S = a * b
2. Формула для нахождения площади треугольника:
S = (a * h) / 2
3. Формула для нахождения объема прямоугольного параллелепипеда:
V = a * b * h
4. Формула для нахождения площади окружности:
S = π * r2
5. Формула для нахождения длины окружности:
L = 2π * r
6. Формула для нахождения площади параллелограмма:
S = a * h
7. Формула для нахождения площади трапеции:
S = ((a + b) * h) / 2
8. Формула для нахождения периметра прямоугольника:
P = 2a + 2b
9. Формула для нахождения периметра треугольника:
P = a + b + c
Запомните эти формулы и применяйте их во время подготовки к ОГЭ по математике. Это поможет вам быстро и верно решать задачи и достичь высоких результатов на экзамене.
Квадратные уравнения и корни

Для решения квадратного уравнения используется формула дискриминанта:
D = b^2 - 4ac
Дискриминант позволяет определить, сколько корней имеет уравнение:
- Если D > 0, то уравнение имеет два различных корня: x1 и x2.
- Если D = 0, то уравнение имеет один корень: x.
- Если D < 0, то уравнение не имеет корней.
Формулы для нахождения корней квадратного уравнения:
- Если D > 0, то корни вычисляются по формуле:
- Если D = 0, то корень находится по формуле:
- Если D < 0, то корней нет.
x1 = (-b + √D) / (2a)
x2 = (-b - √D) / (2a)
x = -b / (2a)
Запомните эти формулы и учитесь применять их к разным квадратным уравнениям. Практика и самостоятельные задания помогут вам освоить эту тему и успешно справиться с вопросами на экзамене по математике.
Пропорциональные и непропорциональные зависимости

В пропорциональных зависимостях одна величина может быть выражена через другую по определенному правилу. Например, если известно, что 20 яблок стоят 100 рублей, то можно вычислить, сколько стоит 1 яблоко.
Если в пропорциональной зависимости одна величина увеличивается в n раз, то вторая величина также увеличивается в n раз. Это правило можно записать в виде формулы:
a/b = c/d
где a и b представляют собой первую величину, а c и d – вторую величину.
Непропорциональные зависимости, напротив, описывают ситуации, когда изменение одной величины не приводит к изменению другой величины в постоянном отношении. Например, если на автомобильный путь влияет не только время движения, но и скорость, то мы имеем дело с непропорциональной зависимостью.
На ОГЭ можно столкнуться с задачами, где необходимо определить, является ли данная зависимость пропорциональной или непропорциональной, а также проанализировать ее график или построить таблицу значений.
Знание формул и правил пропорциональных и непропорциональных зависимостей позволяет решать такие задачи логично и быстро. Поэтому стоит обратить особое внимание на эту тему при подготовке к ОГЭ по математике.
Площади и объемы геометрических фигур
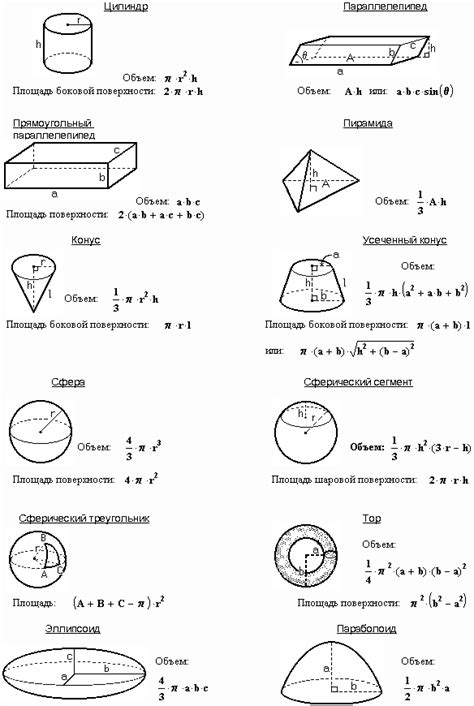
На ОГЭ по математике часто встречаются задачи, связанные с рассчетом площади и объема геометрических фигур. Поэтому необходимо знать некоторые формулы для успешного решения таких задач.
| Фигура | Формула площади | Формула объема (если применимо) |
|---|---|---|
| Квадрат | S = a^2 | - |
| Прямоугольник | S = a \cdot b | - |
| Треугольник | S = \frac{1}{2} \cdot a \cdot h | - |
| Параллелограмм | S = a \cdot h | - |
| Трапеция | S = \frac{1}{2} \cdot (a + b) \cdot h | - |
| Круг | S = \pi \cdot r^2 | - |
| Пирамида (прямая) | - | V = \frac{1}{3} \cdot S_{\text{основания}} \cdot h |
| Цилиндр | - | V = \pi \cdot r^2 \cdot h |
| Конус | - | V = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h |
| Шар | - | V = \frac{4}{3} \cdot \pi \cdot r^3 |
Запомните эти формулы, особенно для наиболее распространенных фигур, и не забудьте применить их при решении задач по площадям и объемам на ОГЭ по математике.
Тригонометрические функции и их значения
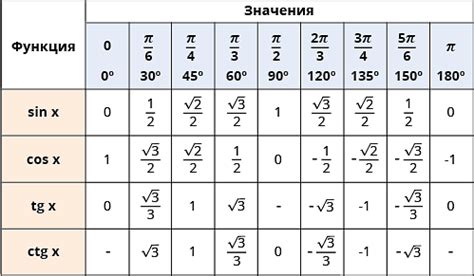
В тригонометрии существует несколько основных тригонометрических функций, которые часто встречаются в задачах на ОГЭ по математике. Важно знать их значения для стандартных углов.
- Синус (sin):
- sin(0) = 0
- sin(30°) = 0.5
- sin(45°) = √2/2
- sin(60°) = √3/2
- sin(90°) = 1
- Косинус (cos):
- cos(0) = 1
- cos(30°) = √3/2
- cos(45°) = √2/2
- cos(60°) = 0.5
- cos(90°) = 0
- Тангенс (tg):
- tg(0) = 0
- tg(30°) = √3/3
- tg(45°) = 1
- tg(60°) = √3
Вероятность и комбинаторика

Формула для расчета вероятности события:
| Вид события | Формула |
|---|---|
| Событие A считается равновероятным | P(A) = N(A) / N, где N(A) - число благоприятных исходов, N - общее число исходов |
| Событие A считается не равновероятным | P(A) = m / n, где m - число благоприятных исходов, n - общее число исходов |
Принципы комбинаторики:
| Вид комбинаторного объекта | Формула | Обозначение |
|---|---|---|
| Перестановка без повторений | Pn = n!, где n - число элементов | Pn |
| Сочетание без повторений | Cnk = n! / (k!(n-k)!), где n - число элементов, k - число элементов в комбинации | Cnk |
| Размещение без повторений | Ank = n! / (n-k)!, где n - число элементов, k - число элементов в размещении | Ank |
Запомните эти формулы и принципы комбинаторики, так как они являются фундаментальными для решения задач по вероятности на ОГЭ. Тренируйтесь на разнообразных задачах и вырабатывайте навык применения этих знаний.



