Когда мы говорим о десятках, а то и сотнях переменных, они все становятся неотъемлемой частью сложных математических моделей, используемых в физике, экономике, биологии и других науках. Очень часто мы хотим узнать, как изменяется функция, когда мы изменяем одну из этих переменных, при этом все остальные сохраняются постоянными. Именно для такого анализа нам и нужны дифференциальные операторы dz/dx и dz/dy.
dz/dx - производная функции z по переменной x. Она говорит нам, какая будет изменение функции z, когда мы будем изменять переменную x. Если dz/dx положительна, то функция z возрастает с ростом x, если отрицательна - то убывает. Но это лишь одна из множества информации, которую можем получить с помощью этой производной.
Аналогично, dz/dy - производная функции z по переменной y. Она позволяет проанализировать изменение функции z при изменении переменной y, позволяет понять, как связаны между собой эти две переменные. Опять же, от знака dz/dy зависит поведение функции z: возрастет она или убывает при изменении y.
Используя дифференциальные операторы dz/dx и dz/dy, мы получаем возможность более глубоко изучать функции и описание сложных систем, а также предсказывать их поведение в зависимости от изменений переменных. Это важный инструмент для любого исследователя, стремящегося к более точным и полным результатам.
Основное понятие dz dx и dz dy

Рассмотрим ключевые концепции, связанные с dz dx и dz dy, чтобы лучше понять, как они применяются и как взаимодействуют в различных областях.
dz dx: Этот термин связан с изменением функции (z) по оси x. Он показывает, какое значение функции изменяется при изменении направления по оси x.
dz dy: Этот термин, наоборот, описывает изменение функции (z) по оси y. Он демонстрирует, какое значение функции меняется при изменении направления по оси y.
Понимание и применение dz dx и dz dy имеет большое значение в области дифференциального исчисления и математического моделирования. Когда функция зависит от двух или более переменных, dz dx и dz dy помогают определить ее изменение в различных направлениях. Знание этих концепций позволяет анализировать функции, оптимизировать процессы и предсказывать результаты экспериментов.
Например, рассмотрим график функции, описывающей поверхность земли. Используя dz dx, мы можем определить, как изменится высота поверхности, двигаясь по оси x, а с помощью dz dy - аналогично, но по оси y. Это знание может быть использовано при планировании строительства дорог, определении рельефа местности и других географических и инженерных задачах.
Сущность и роль dz dx и dz dy в математике

Если мы обратим внимание на представление функций с несколькими переменными, то можно заметить, что каждая переменная вносит свой вклад в их значения. Чтобы выразить этот вклад и оценить влияние каждой переменной, применяются частные производные, такие как dz/dx (производная функции z по переменной x) и dz/dy (производная функции z по переменной y).
dz/dx и dz/dy представляют собой меру изменения функции z в зависимости от изменения переменных x и y соответственно. Они позволяют оценить, как изменится значение функции z, если мы внесем небольшие изменения в значения переменных x и y. Таким образом, dz/dx и dz/dy помогают нам понять, как вклад каждой переменной влияет на результат функции.
Например, рассмотрим функцию z = x^2 + 2xy + y^2. Если мы хотим оценить влияние переменной x на эту функцию, то можем вычислить dz/dx. Аналогично, если интересует влияние переменной y, то можем вычислить dz/dy. Результаты вычислений dz/dx и dz/dy позволяют нам определить, например, в какой точке функция достигает максимума или минимума, а также выбрать оптимальные значения переменных для достижения желаемого результата.
Использование dz/dx и dz/dy в математике является важной составляющей для анализа функций с несколькими переменными. Они позволяют нам разбить функцию на составляющие и понять, как каждая из них влияет на общий результат.
Примеры использования dz dx и dz dy
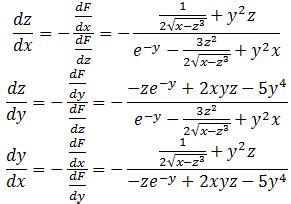
В данном разделе мы рассмотрим конкретные примеры применения dz dx и dz dy, которые позволяют измерять изменение функции по отдельным осям. Они играют важную роль в математическом анализе, где помогают оценить скорость изменения функции относительно каждой из переменных.
Представим ситуацию, где некая функция описывает температуру воздуха в зависимости от двух факторов: времени и географической широты. В данном случае, dz dx будет показывать, насколько быстро меняется температура воздуха при изменении времени, а dz dy – при изменении широты.
- Например, при анализе данных глобального изменения климата, dz dx может помочь установить, как изменяется температура каждый год и выявить тренды климатических изменений.
- Аналогично, dz dy может использоваться для определения изменений температуры воздуха в разных регионах мира и их сравнения между собой.
- В области экономики, dz dx и dz dy могут быть применены для анализа спроса на товары или услуги при изменении цены или дохода потребителей соответственно.
Таким образом, dz dx и dz dy являются мощными инструментами для изучения зависимостей между переменными и анализа их изменений. Они позволяют получить количественные данные о скорости изменения функции относительно отдельных переменных и применяются в различных областях науки и бизнеса.
Практические примеры для лучшего усвоения принципов dz dx и dz dy
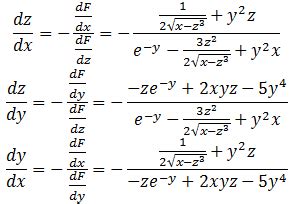
В данном разделе будут представлены практические примеры, которые помогут лучше понять и применить принципы dz dx и dz dy. Здесь мы рассмотрим несколько ситуаций, где эти концепции могут быть полезными, без вдавания в точные определения и теории.
- Пример воздействия на экономику: предположим, что у вас есть некоторые данные о росте ВВП и инвестициях в разные регионы страны. Вы хотите определить, как изменение инвестиций (dx) влияет на изменение ВВП (dz). Здесь dx и dz соответствуют изменению инвестиций и ВВП соответственно.
- Пример в анализе климатических изменений: предположим, что вы исследуете изменение температуры (dz) в зависимости от изменения широты (dy) и долготы (dx). Изучая эти зависимости, вы можете более точно предсказывать климатические изменения в разных регионах.
- Пример прогнозирования спроса и предложения: предположим, что вы анализируете данные о ценах (dz), количестве спроса (dz) и изменении дохода (dx), чтобы предсказать, какое количество товара будет потребляться при данных изменениях.
Это лишь несколько примеров, которые иллюстрируют применение принципов dz dx и dz dy в практических ситуациях. Изучение этих концепций позволяет более точно анализировать и предсказывать различные явления и процессы, а также принимать обоснованные решения на основе математической моделирования.
Основные правила использования dz dx и dz dy
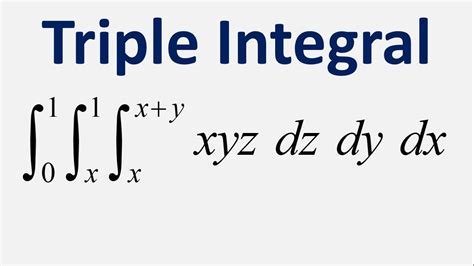
В кратком определении, dz dx и dz dy представляют собой частные производные функции, где dz обозначает изменение функции по оси z, а dx и dy - изменение по соответствующим осям x и y.
Основное правило использования dz dx и dz dy заключается в понимании, что эти дифференциалы являются частными производными функции по отдельным переменным. На практике это означает, что мы можем измерять изменение функции вдоль каждой отдельной оси.
При использовании dz dx и dz dy необходимо учитывать также правила дифференцирования, которые позволяют нам вычислять значения этих дифференциалов. Например, если у нас есть функция f(x, y, z), то мы можем вычислить dz dx и dz dy с помощью правил дифференцирования, определенных для этой функции.
Частные производные dz dx и dz dy часто используются для изучения изменений функции в пространстве или на поверхности. Например, в физике они могут использоваться для вычисления градиента векторного поля или для определения направления изменения температуры в пространстве.
Важно отметить, что правила использования dz dx и dz dy не ограничиваются только двумерными или трехмерными пространствами. Они также могут быть применены в случае функций с большим числом переменных и в более сложных задачах.
| Пример использования dz dx и dz dy: |
|---|
| Предположим, у нас есть функция f(x, y) = x^2 + 2y. Для определения dz dx и dz dy сначала вычисляем частные производные: |
| dz dx = 2x |
| dz dy = 2 |
| Это означает, что при изменении значения x на единицу, значение функции f изменится на 2x, а при изменении значения y на единицу, значение функции f изменится на 2. |
Основные правила и ограничения, связанные с dz dx и dz dy
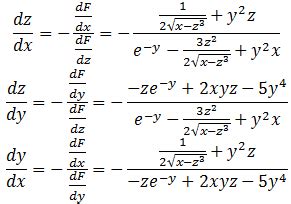
Во-первых, для корректного применения dz dx и dz dy необходимо быть внимательным к контексту. Каждое из этих понятий имеет специфическую семантику и применяется в определенных ситуациях. Понимание контекста поможет правильно интерпретировать и использовать данные формулы.
Во-вторых, важно помнить, что dz dx и dz dy описывают изменение функции по отношению к соответствующим переменным. Для правильного применения этих понятий необходимо учитывать их математические свойства и принципы.
Одним из ограничений, связанных с dz dx и dz dy, является их применимость только в случаях, когда функция имеет непрерывные производные. В противном случае, использование данных понятий может привести к ошибкам и некорректным результатам.
Дополнительным ограничением является необходимость правильной интерпретации знаков перед dz dx и dz dy. Знаки указывают на направление изменения функции по отношению к соответствующим переменным и могут иметь важное значение при анализе и применении этих понятий.
Расхождение между dz dx и dz dy

Знание различий между dz dx и dz dy имеет важное значение в математических и физических исследованиях, где проводится анализ изменения функций относительно различных переменных. Оба понятия представляют собой производные функций по отношению к определенным переменным, но их специфика и применение имеют свои особенности.
При использовании dz dx производная функции рассчитывается по отношению к переменной x, в то время как dz dy относится к производной функции относительно переменной y. Различие в выборе переменных влияет на способ интерпретации и применение результатов. Понимание этих различий необходимо для точного анализа функций и дальнейших вычислений.
| dz dx | dz dy |
|---|---|
| Производная по переменной x | Производная по переменной y |
| Интерпретация изменений функции относительно x | Интерпретация изменений функции относительно y |
| Применимо в случаях, когда изменения функции связаны с изменениями x | Применимо в случаях, когда изменения функции связаны с изменениями y |
Вопрос-ответ

Что означают символы dz, dx и dy в математике?
Символы dz, dx и dy в математике обозначают дифференциалы переменных. Dz соответствует дифференциалу функции z, dx - дифференциалу функции x, а dy - дифференциалу функции y.
Какие принципы лежат в основе использования dz dx и dz dy в математике?
Основным принципом использования dz dx и dz dy в математике является представление функции как суммы бесконечно малых изменений. Значения dz, dx и dy позволяют определить, в каком направлении и насколько изменится функция при незначительном изменении переменных.
Можете привести примеры использования dz, dx и dy в математике?
Конечно! Например, при нахождении производной функции по x или y, мы используем символы dx и dy. Еще один пример - в задачах оптимизации, где нужно найти экстремум функции, dx и dy используются для нахождения приращений переменных и сравнения их влияния на значение функции.



